
公開日2021/02/02 更新日2021/02/28 No.20追加
どうも、塾講師のこうです。
このページに来て頂きありがとうございます。
あなたが受験生(中3)ならNo.1-10から順番に見ることをおすすめします。
↓↓↓↓↓↓↓↓↓↓
www.jukuteacher.com
No.11からは2021年度入試で範囲外(大阪で)になった内容も少しずつ載せていきます!
基本的には、偏差値50を超えることをテーマに問題を選んでいます。
中には簡単だったり、難しい問題があったりすると思います。
ただ、そういう問題を選んでいるのは、
ミスが多い問題だったり、僕が解けて欲しい問題であったりします。
解き方の解説を読むだけでも価値があるようにしていきたいと思っています。
(実際に価値があるかどうかは謎ですが笑)
ぜひ利用できるものは利用していってください。
では、頑張ってください!
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
- ■偏差値50突破への道No.11
- 《答え》偏差値50突破への道No.11
- ■偏差値50突破への道No.12
- 《答え》偏差値50突破への道No.12
- ■偏差値50突破への道No.13
- 《答え》偏差値50突破への道No.13
- ■偏差値50突破への道No.14
- 《答え》偏差値50突破への道No.14
- ■偏差値50突破への道No.15
- 《答え》偏差値50突破への道No.15
- ■偏差値50突破への道No.16
- 《答え》偏差値50突破への道No.16
- ■偏差値50突破への道No.17
- 《答え》偏差値50突破への道No.17
- ■偏差値50突破への道No.18
- 《答え》偏差値50突破への道No.18
- ■偏差値50突破への道No.19
- 《答え》偏差値50突破への道No.19
- ■偏差値50突破への道No.20
- 《答え》偏差値50突破への道No.20
■偏差値50突破への道No.11

使用問題:2017〜2019年公立高校入試過去問(以下同様)
使用問題集:2021 2022年受験用 全国高校入試問題正解 分野別過去問 735題 数学 数と式・関数・資料の活用
この問題集は難易度の高い問題もたくさんありますが、基本的な問題も数多くあります。
よって、
基本的な問題を中心に解くことで基礎固めにも十分役立つのでおすすめ
※基本的な問題の見分けがつかない場合は、先生にどの問題ができたらいいか聞くといいですね。ただ、いきなり全部を見るのは無理なので分野ごとに聞くようにしましょう。
使用問題集:2021 2022年受験用 全国高校入試問題正解 分野別過去問 411題 数学 図形
《答え》偏差値50突破への道No.11
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
《大1問》
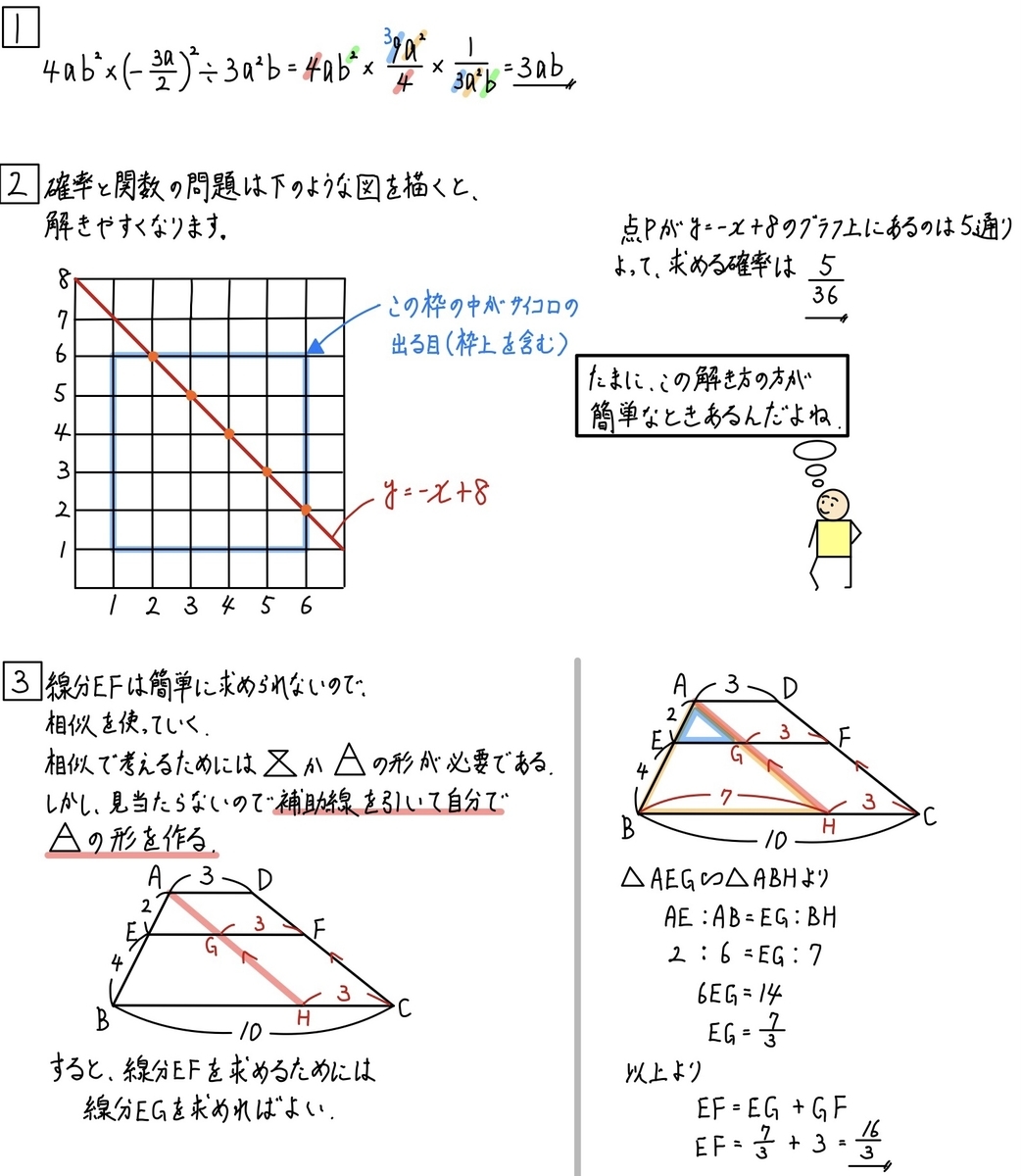
確実に正解してほしい問題です。
しかし、見落とし、計算ミスなどが起こりやすい問題です。
油断せずに丁寧に計算することを心がけていきましょう!
《第2問》
僕はこの問題をグラフを使って解くかと聞かれたら、Noです笑
ただ、「この問題では」ですけど。
実際に、グラフを使わないと求めにくい問題が出たりします。
その時に、1つのやり方だけを身につけるのではなくて、状況に応じた解き方ができるようになってほしいという思いを込めてこの解き方を載せました。
数学ができる人の様子を見ていると
状況に応じて解き方を変えることができていることが多いです。
ぜひいろんな解き方を身につけてくださいね!
《第3問》
この問題は見たことありますよね?
学校の問題集で必ず載っています。
もちろん、塾の問題集でも載っています。
定期試験でも出題する先生がほとんどのはずです。
つまり、できないといけない問題です。
できた人は大変素晴らしい!
でも、できなかった人いますよね?
入試に合格する近道は
できない問題をできるようにしていくこと
です。
僕がここで解説を載せている問題は、
偏差値50を超えている人は大体解けている問題を中心に選んでいます。
ぜひせっかくここにたどりついたなら
思いっきり利用してくださいね!
できないのは恥ずかしいことじゃない!
できないままにするのが恥ずかしいことなんだ!
■偏差値50突破への道No.12

《答え》偏差値50突破への道No.12
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
《大1問》
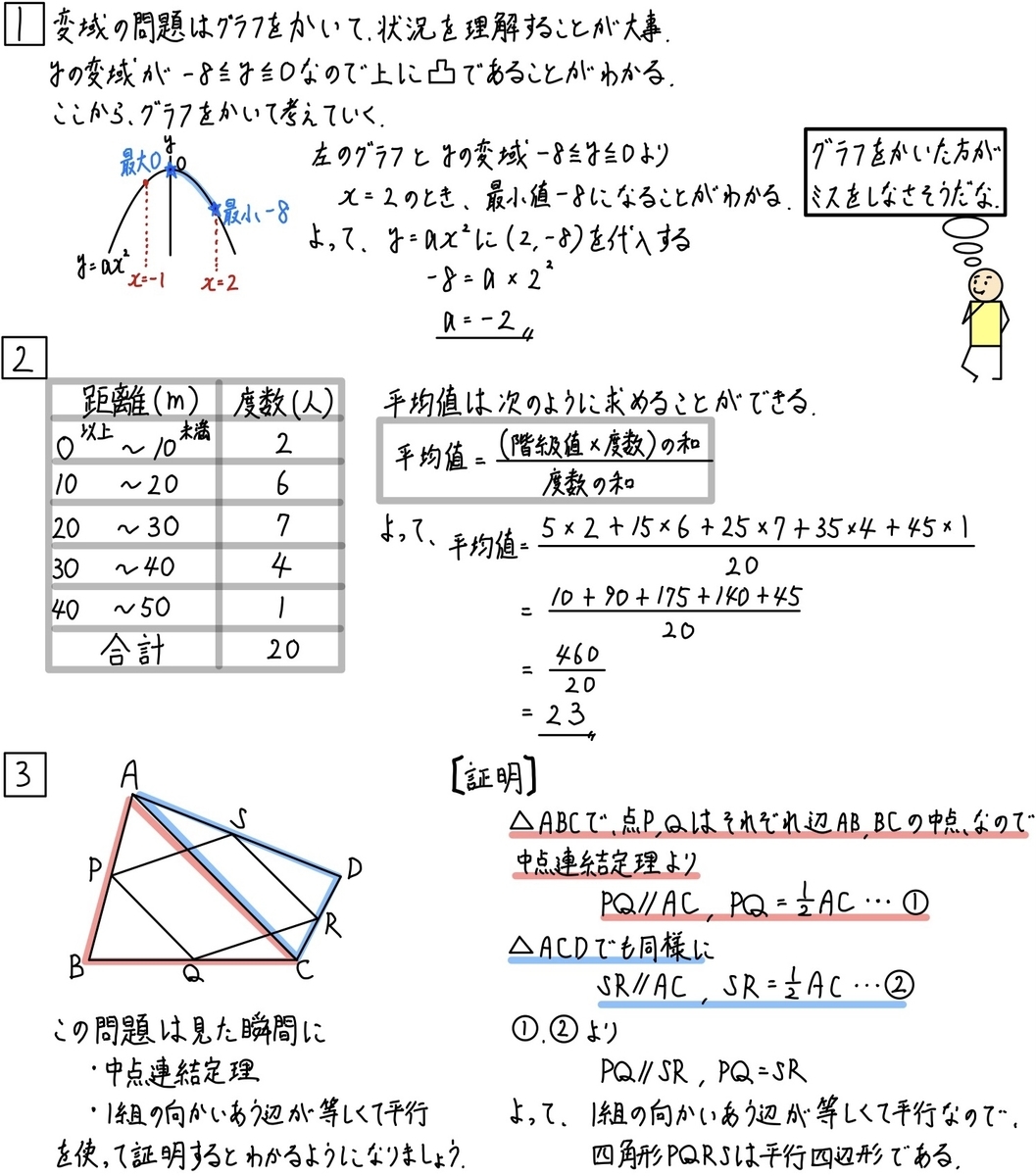
この問題は非常にミスが多い問題です。
特に、グラフを描かないで解く人は要注意ですね。
そういう人は一次関数の似たような問題で間違えたりもします。
入試は早く解けた方がいいですが
それ以上に正確に解くことの方が何倍も大事です!
なるべくグラフを描いて状況を確かめながら解くようにしましょう!
《第2問》
平均値には2つの求め方があります。
1つは小学校の時に習いますね。
もう1つは中学校で習います。
(2021年から小学生で両方習うようになりましたが)
中学で習うのは、階級値を使うやり方です。
これはやり方を知らないと絶対に解けないです。
数学で安定して点数を取るためには
知っていれば解ける問題は全てできるようにしましょう。
これだけで、最低限の点数は確保できるようになりますよ!
《第3問》
この問題は見覚えありますよね?笑
入試問題より定期試験で出題されることがほとんどです。
しかし、このように入試でも問われたりします。
中点連結定理と平行四辺形の性質を使って証明しなければなりませんが
図形が変わっても書くことはほとんど変わりません笑
だから、確実に正解して欲しい問題だと僕は思っています。
また、中点連結定理や平行四辺形の性質はしっかりわかっていますか?
分かっていなければ、今すぐ教科書を開いて確認しましょう!
中点連結定理は、中3の教科書
平行四辺形の性質(5つ)は、中2の教科書
に載っていますよ!
■偏差値50突破への道No.13
《答え》偏差値50突破への道No.13
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
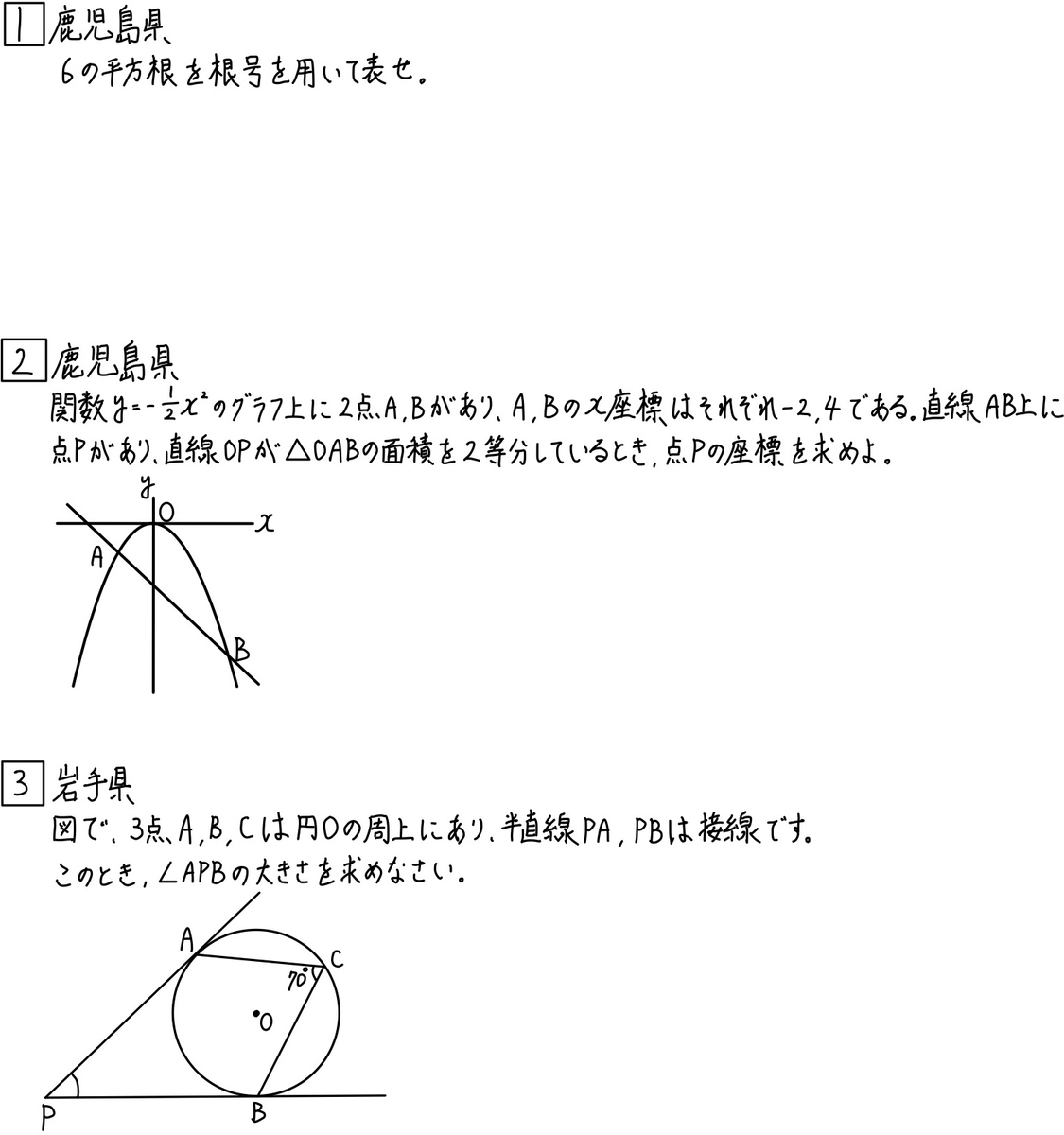
《大1問》
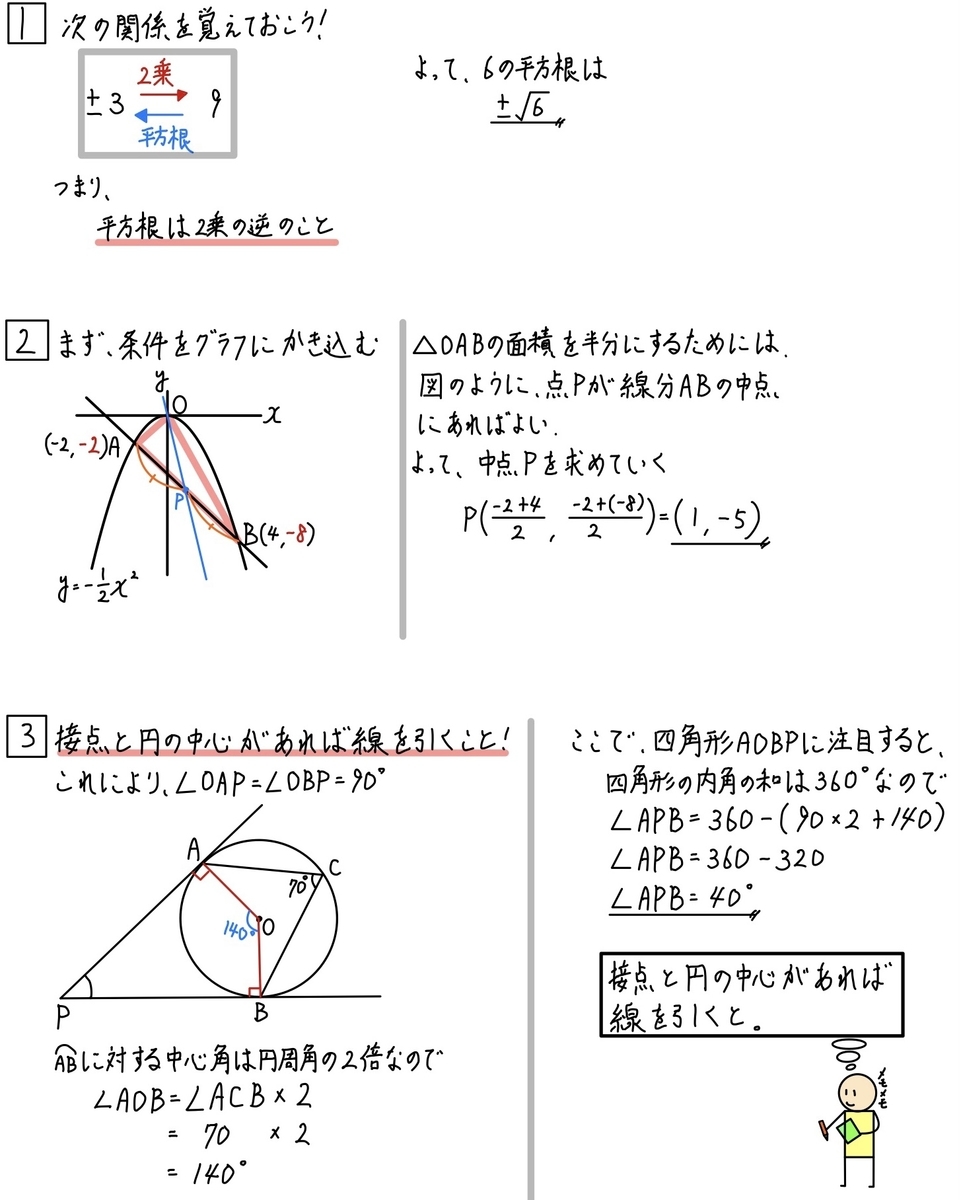
±を忘れませんでしたか?
平方根を習いたての時は忘れませんが、時間が経つと忘れる人が続出します。
こういったミスをしないように心がけましょうね!
《第2問》
中点の求め方は大丈夫ですか?
意外と、中3でもこの求め方を知らないことが多いです。
学校で習っているはずなんですが笑
中点の求め方を知らない生徒には次のような確認をします。
5と17の真ん中の数字は何?
答えられましたか?
パッと求められないなら、中点の求め方を知らないと即わかります。
この中点を求めたいなら、次の式でできます。
(5+17)÷2=11
つまり、中点は11ですね。
簡単ですよね。
ぜひ覚えておきましょう!
《第3問》
この問題は、あることをしなければ絶対に解けません。
それは
接点と円の中心を結ぶこと
です。
もうこの2つが図形に出てきたら、結びたくなって仕方なくなってほしいくらいです笑
なぜ結ぶのかというと、直角ができるからですね。
これをするだけで解けちゃいます!
覚えておきましょう!
■偏差値50突破への道No.14

《答え》偏差値50突破への道No.14

解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
《大1問》
この問題は少し難しく感じたかもしれませんね。
こういう問題は、
どういう状況になればいいのか
をしっかり理解する必要があります。
力技で時間をかけて解くこともできると思いますが、
できればもっと良い解き方はないかなって思うようにしてください。
その良い解き方が
解説を見てわかればそれで良いですし
解説を見ても分からなければ先生に聞きにいきましょう。
こういう時にこそ、先生を一番利用すべきですね!
《第2問》
確率の問題で注意しなければならないのは、
「並び方」か「選び方」のどちらの問題なのかをしっかりすることです。
並び方であれば、順番を考えなければなりません。
例えば、12と21は、十の位と一の位を入れ替えただけですが意味が変わりますよね。
選び方であれば、順番を考える必要はありません。
例えば、3と4を選ぶのと、4と3を選ぶのは変わりませんよね。
状況によって、これ以外にも考えなければならないこともあります。
確率は、何となくで解くのではなく、しっかり書き出して解くようにしてくださいね!
《第3問》
これは必ず覚えておいてほしい問題です。
最短距離を求める問題は、
展開して
考えていきましょう!
展開することさえ知っていれば、
簡単に解けることが非常に多いです。
■偏差値50突破への道No.15

《答え》偏差値50突破への道No.15
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
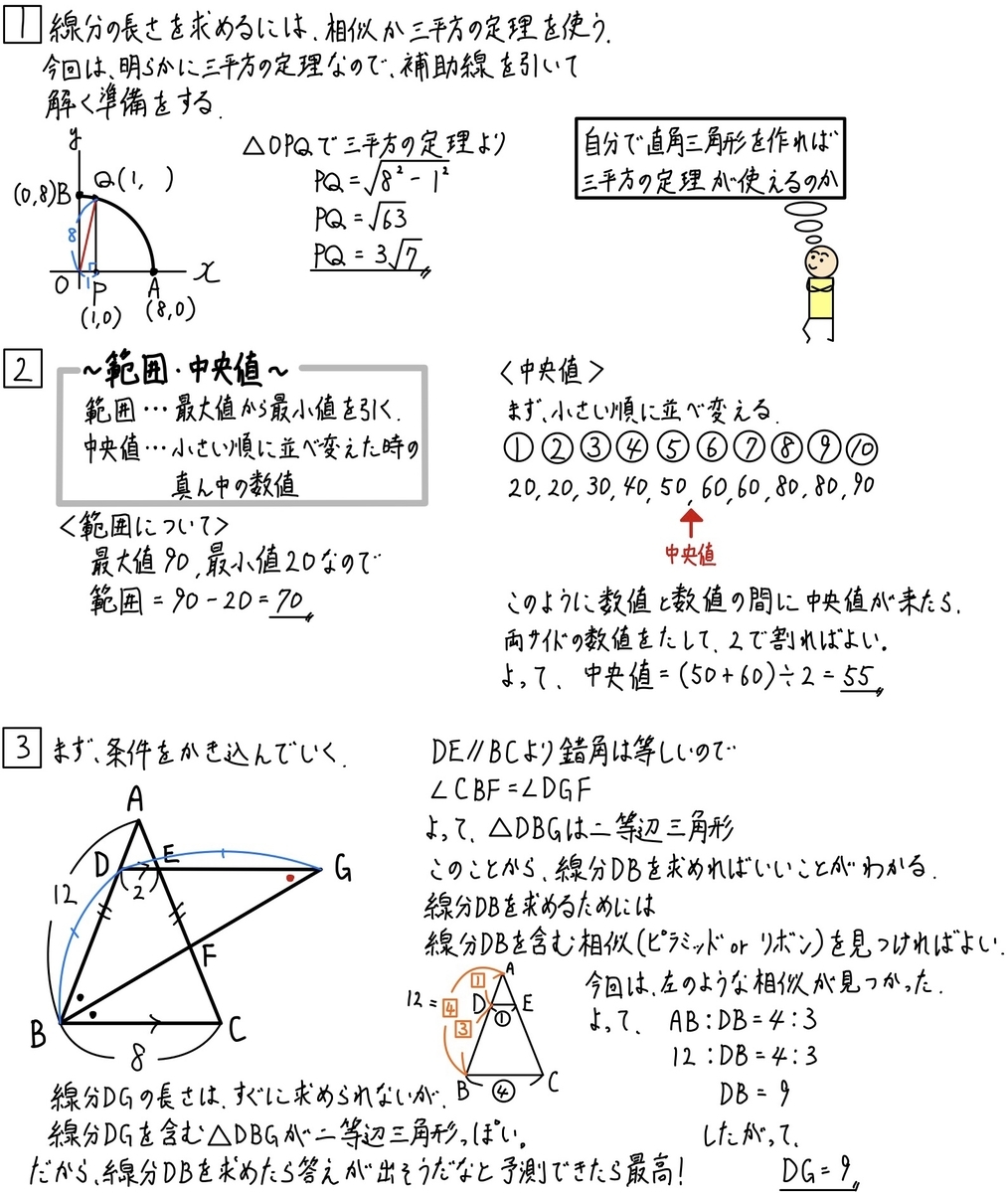
《大1問》
長さを求めるためには
三平方の定理か相似
を使って解くことがほとんどです。
今回の場合、
相似は明らかに使えないので
三平方の定理を使って解けば良いのか
とわかればバッチリですね。
このあたりができるようになるには
問題数をこなせば必ず分かるようになります。
「あ、このパターンはあの解き方だな」
みたいに笑
この感覚が出てきたら、偏差値50を下回ることはなくなるはずです。
《第2問》
範囲の求め方は大丈夫でした?
中央値は結構解き方を覚えているのに
範囲の求め方を忘れてる
って人が多いんですよね。
これは、問題集に収録されている問題数の差が影響しているのだと思います。
範囲を求める問題は少ないのに
中央値を求める問題はたくさんありますからね笑
だから、しばらく解かなくても忘れないくらい復習を何回もしましょうね!
《第3問》
この問題は少し難しかったですね。
できなくても落ち込まないでくださいね。
解説を見て解き方が理解できたら十分です。
(偏差値50を突破するためには)
なぜ難しく感じるのか。
それは
・平行線の錯覚は等しくなる
・二等辺三角形を見つける
・相似の形(ピラミッドかリボン)を見つける
など
考えることがたくさんあるから。
このうち、1つでも分からないことがあれば正解に辿り着きません。
1つでも2つでも見つけれる努力をしましょう!
■偏差値50突破への道No.16

《答え》偏差値50突破への道No.16
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
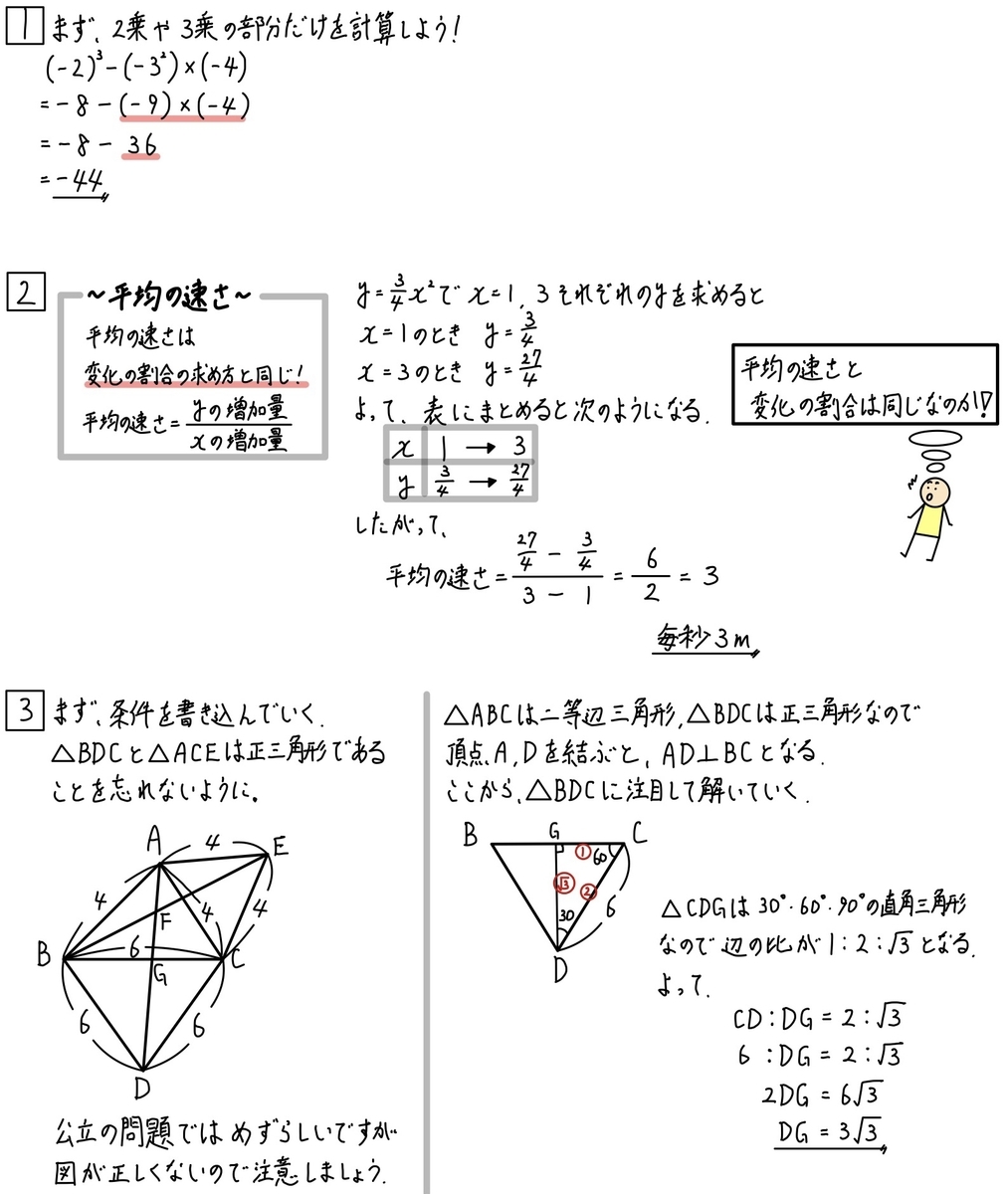
《大1問》
簡単な問題ですが
符号のミスが出やすい問題です。
こういう問題こそ、1つ1つ丁寧に取り組みましょう
早く解けても、不正解なら0点ですからね。
《第2問》
平均の速さの求め方は知っていましたか?
これは、変化の割合と求め方が同じなんです。
これさえ知っていれば、この問題は解けましたね!
いろんな問題を解いて、こういう知識を増やして入試に挑む準備をしていきましょう!
《第3問》
この問題は問題なく解けましたか?
僕は、なんか違和感があって一瞬止まってしまいました笑
公立の場合、正確な図をしっかり全て描いてあることがほとんどです。
しかし、今回は正確な図を描いてありませんでした。
(もしかしたら、自分で図を描いて解いてほしいという意図が含まれていたかもしれませんね)
ただ、私立では図が正確ではないことはちょくちょくあります。
見た目に惑わされずに、正確に条件を読み取って解くことは非常に大事です。
それができていれば、この問題は比較的簡単な問題でしたね。
■偏差値50突破への道No.17

《答え》偏差値50突破への道No.17
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
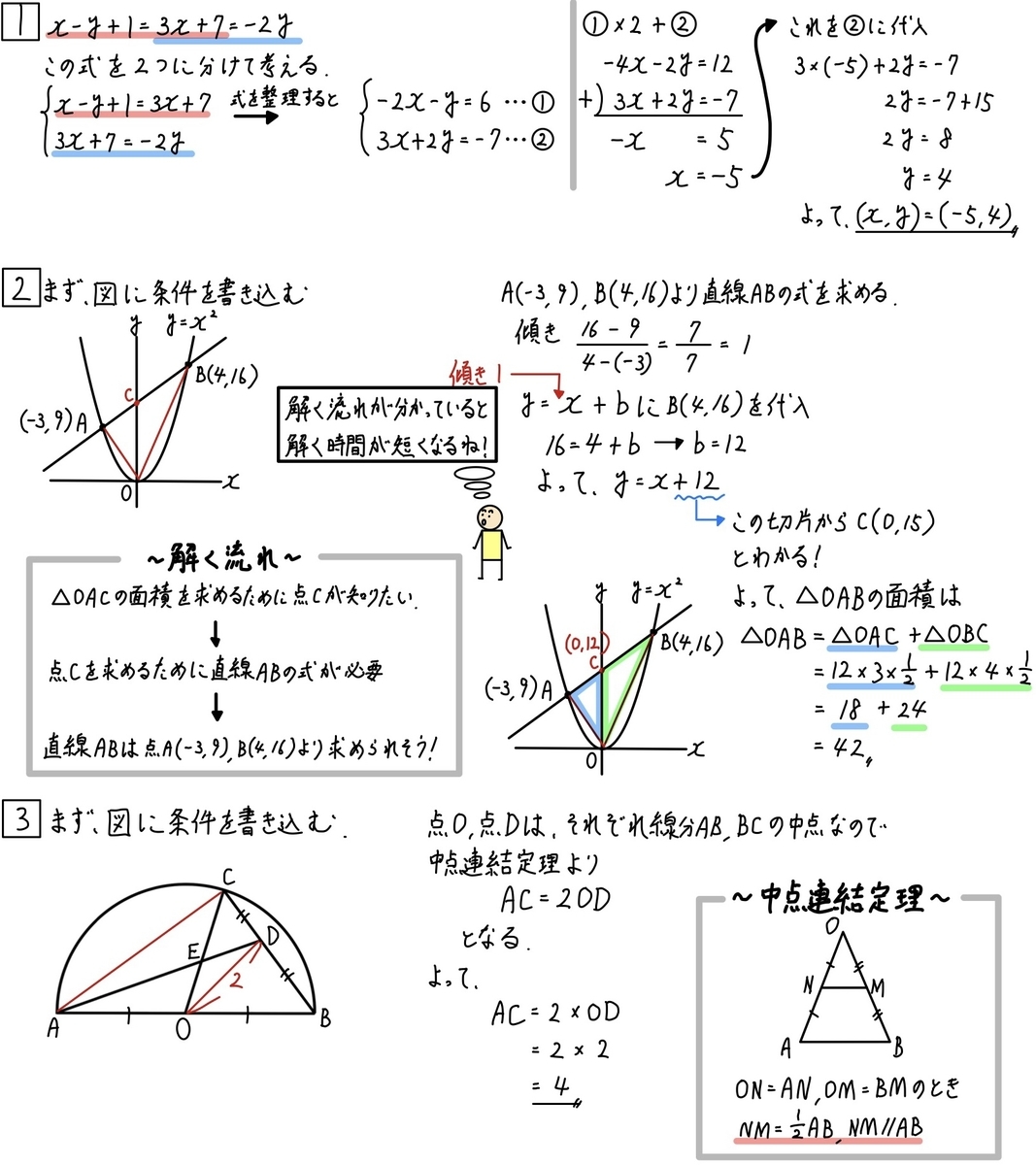
《大1問》
久しぶりに見て解き方を忘れたりしていませんでしたか?
僕は、中3でこの問題の解き方を忘れている生徒を先日見かけました笑
定期的に復習しないと人間は忘れます。
この問題は、1つの式にまとまっています。
これを2つの式に分解して、いつも通りの連立方程式で解くことができるか
がカギの問題でしたね。
ただ、解き方は決まっているのでしっかりできるようにしておきましょう!
《第2問》
この問題は、手前にもう少し小問があり、誘導がありました。
しかし、よくあるパターンなのでそれを省きました。
省いたとしても、そこまで難易度は高くないのでしっかりできるようにしておきましょう。
《第3問》
この問題は、わかる人には超簡単な問題です。
しかし、分からない人は試験中ずっと分からない問題かもしれません。
つまり、差が開く問題です。
入試には、こういった差が開く問題があります。
こういった問題ができるようになれば偏差値50を下回ることはなくなります。
この問題では、中点連結定理(ただの相似で考えても良い)であることさえ分かれば一瞬でした。
こういった気付きは問題を解く量で決まります。
なぜなら、
たくさん解かないと似たような問題がたくさん出題されていることが分からないから。
似たような問題だとわかれば、自然と気付くようになります。
■偏差値50突破への道No.18

《答え》偏差値50突破への道No.18
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
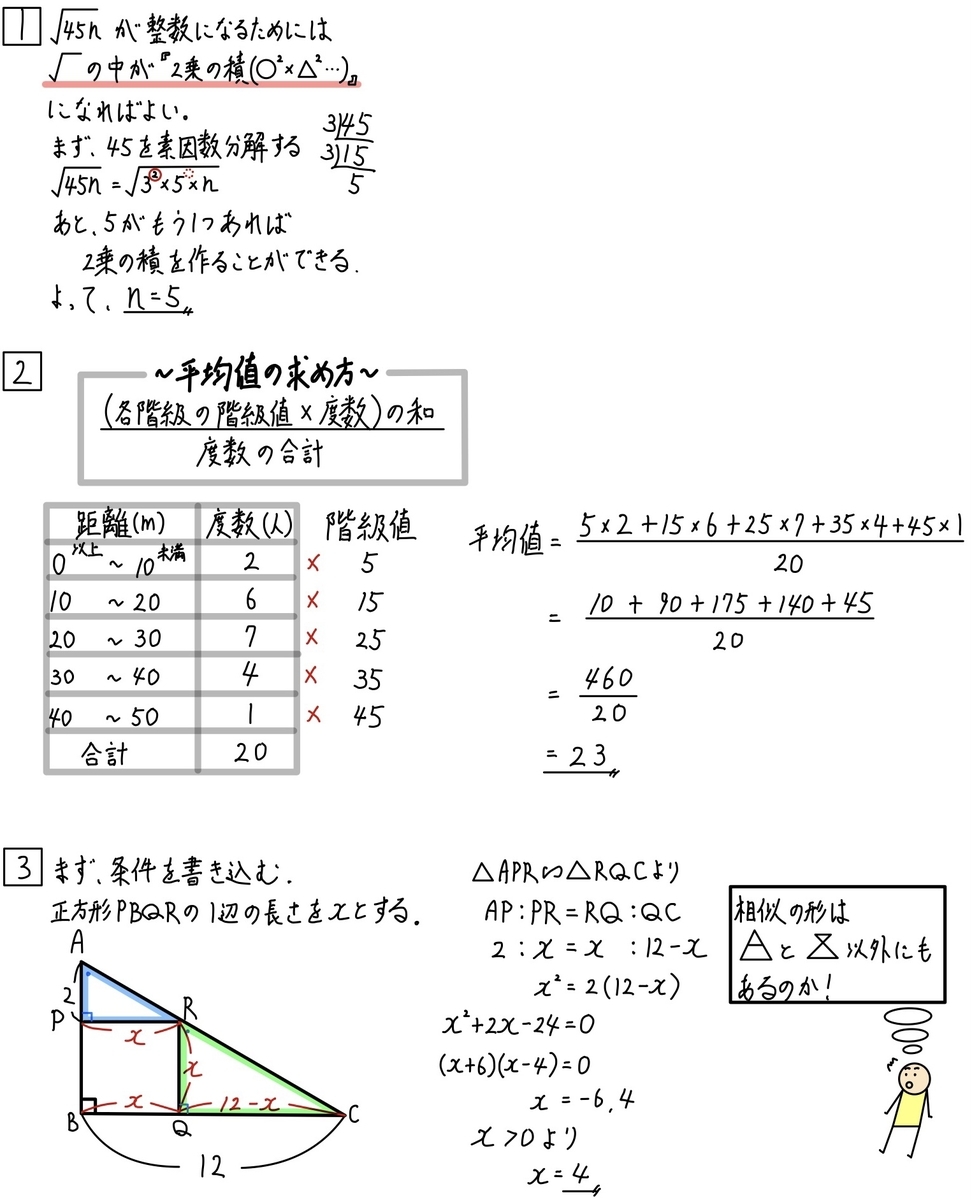
《大1問》
知っていれば簡単な問題ですよね。
でも、解けるだけではなく
「なぜそうなるのか」
をしっかり理解した上で解けるようになってほしいです。
解けるけど機械的に解いているだけの人が多いように感じます。
これだともう1段回難しくすると解けなくなるんです。
もしこの問題が分からない友達がいれば、教えてあげるといいですね。
《第2問》
平均値の解き方は知っていますか?
こう聞くと、知っているという人がほとんどです。
じゃあ、この問題解いてみてというと解けないんですよね笑
平均値には2種類の解き方があります。
1つは小学校で習う解き方
もう1つは中学校で習う解き方(階級値を使うやつ)
ですね。
中学校の解き方がわかっていない人が結構多いので要注意です。
本日、数学が苦手な中3がこのあたりの問題を解いていました。
平均値、中央値、最頻値、範囲の中から正解の数値が書かれている問題を選ぶ問題でした。
全く分からない様子でしたので、1つ1つ確認しながら解きましたが、
あなたは大丈夫ですか??
《第3問》
この問題は、相似を使って解く問題ですね。
僕は、相似の問題だとわかると
ピラミッドかリボンの形を探すように基本的に指導します。
問題の7〜8割はこれで解けてしまうので。
しかし、この問題のように
ピラミッド、リボン以外の時も当然登場します。
この相似を見つけるのが結構難しかったりします。
頑張って見つけれるようになりましょうね!
(この問題は、実は相似のピラミッドが存在します。たまには、違う解き方もありですよね。)
■偏差値50突破への道No.19

《答え》偏差値50突破への道No.19
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
《大1問》
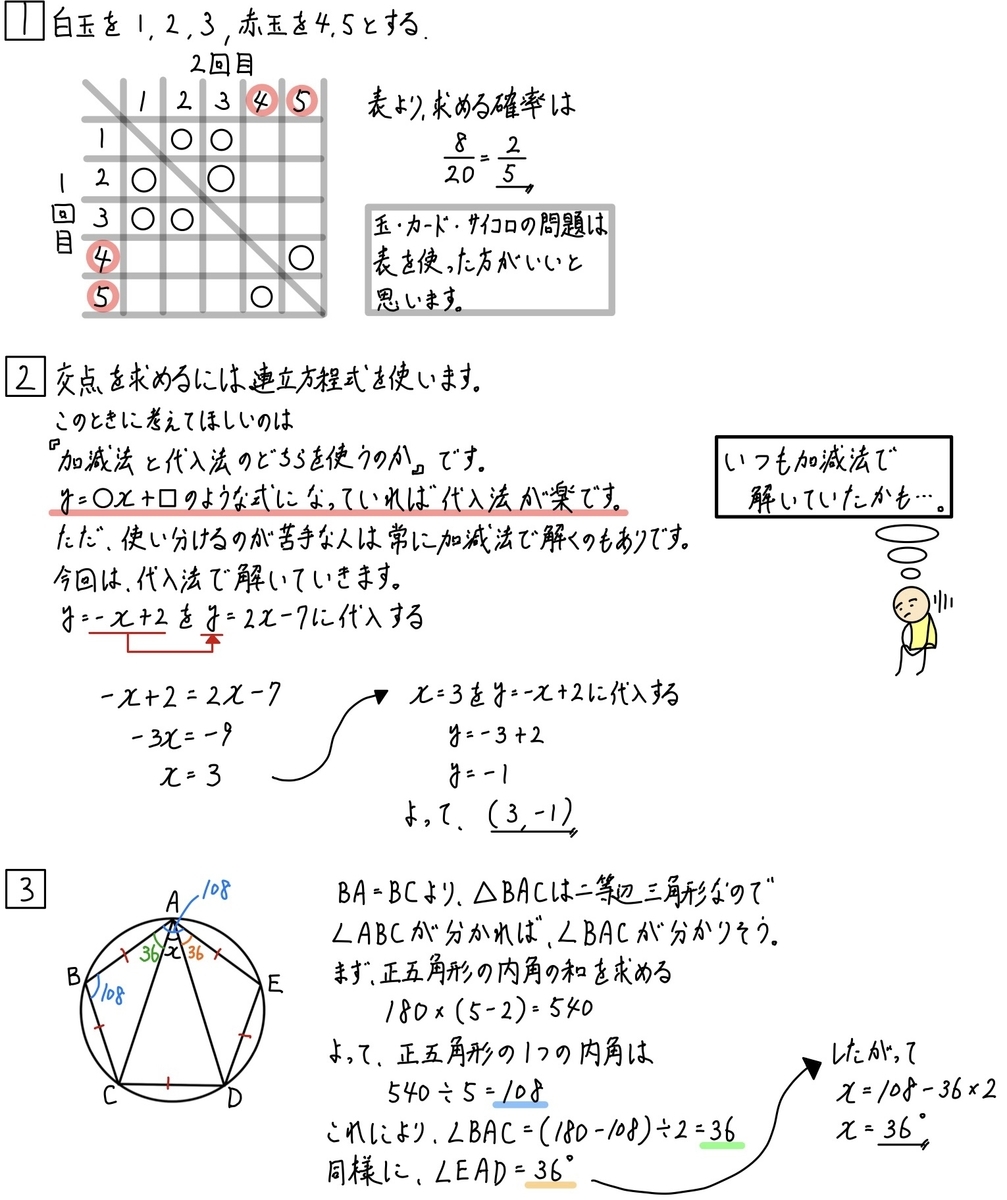
樹形図で解くように指導されることが多いように感じます。
しかし、見落としをしてしまう人が多いように感じます。
学校の先生は、基本的に樹形図推しの印象です。
今の中2の学校の先生は、珍しく表推しですが笑
僕も表推しの先生です笑
僕が、表推しの理由は
・見落としをする人が少ないように感じること
・見直しがしやすいこと
・表に記入すると規則性が出ることが多いのでミスがしにくいこと
という感じです。
ぜひ参考になれば嬉しいです。
《第2問》
これは大丈夫ですよね??
ただ、僕がこの問題を選んだ理由は先生なら分かるかもしれない。
勉強が苦手な子に多いのですが
全部の連立方程式を加減法で解こうとする人が必ず一定数います。
苦手な生徒の場合、加減法だけで解くように指導することは毎年数人います。
しかし、普通以上の成績なのに全部加減法で解こうとする生徒も必ずいます笑
こういった生徒には、もっと楽にできる方法があるってことを知ってほしい。
むしろ、楽してできる良い方法がないかを常に疑ってほしい。
これができる生徒は、必ずと言っていいほどかなり良い成績を取っています。
ぜひ考えながら解いてみてくださいね!
《第3問》
上の解説では、円を使わずに解きました。
もう少し分かりやすく言うと
円周角を使って解けばすぐに解けるというやつです。
まあ、そこまで労力が変わるわけじゃないので上の解説でもいいと僕は思ってますが。
気になる方は、
円周角を使う解き方を考えてみてくださいね!
そして、分からない人は学校か塾の先生に聞いてみてくださいね^^
■偏差値50突破への道No.20
《答え》偏差値50突破への道No.20
解説に何かミスがあれば、下のコメント欄、もしくは、お問合せから教えていただけると嬉しいです。
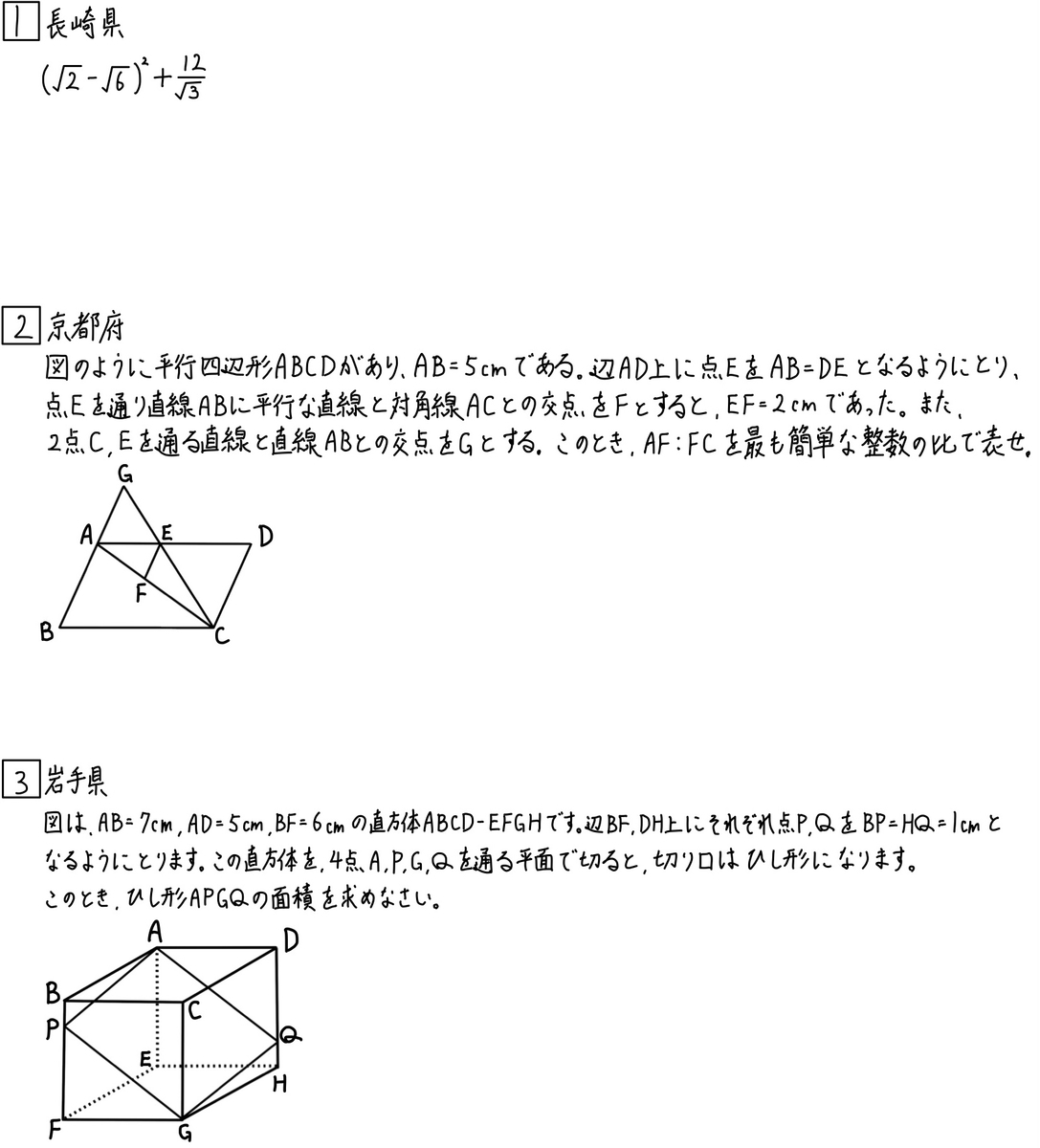
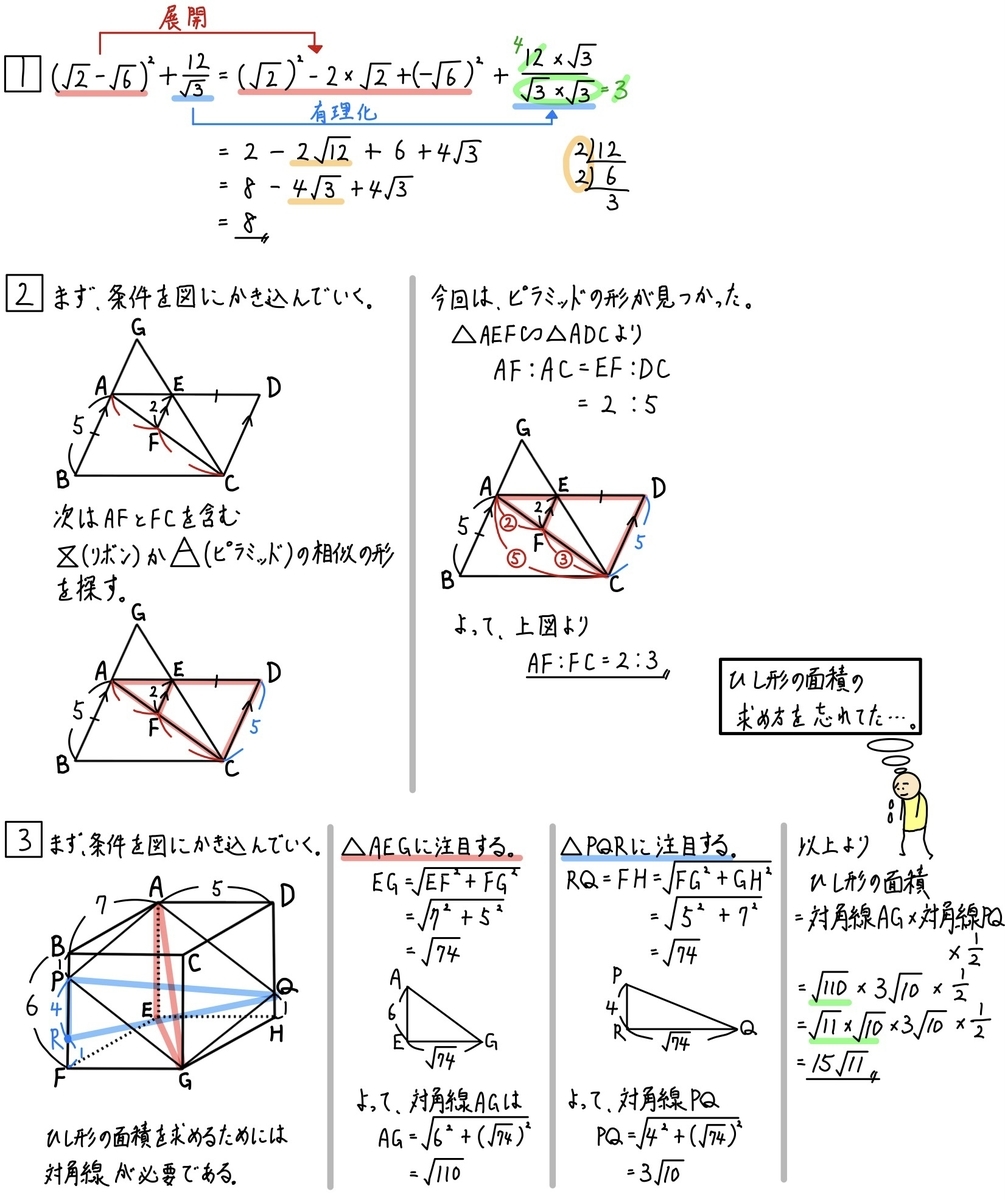
《大1問》
この計算問題はしっかり正解してほしいですね。
ただ、計算ミスは誰にでも起こりえます。
そのミスが本番で出ないようにしっかり準備していきましょうね!
《第2問》
この問題もそこまで難易度は難しくありません。
たまたま塾で扱っている問題と全く同じ問題だったので取り上げてみました。
数学が苦手な人の場合、苦戦しやすいですね。
こういった問題で、最初にしてほしいことは
相似の形(リボンかピラミッド)を見つけること。
もちろん、これ以外のパターンもありますが数は少ないです。
ぜひ、上の解説のように相似の形を見つけて解けるようになってくださいね!
《第3問》
これは意外と取りこぼしが増えそうな問題です。
特にひし形の面積の求め方は覚えていましたか?
意外と中学生でこれを答えられない人は多いです。
ひし形の面積の求め方のように
覚えなければならない公式を覚えていない人は
しっかり入試までに確認して覚えておきましょう!
以上です。
ーーーーーーーーーーーーーーーーーーーー
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。