
公開日2022/03/17
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
自分の勉強のために解説を書いています。
間違い等あればお気軽に指摘してくれると嬉しいです。
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
解説している問題は発表されるまでお待ちください。
第一問
(1)〜(2)解説「計算問題・連立方程式」☆☆

(1)の計算問題は符号のミスが非常に多い問題です。
定期試験で450点以上を取っているような生徒でも間違えています。
この時に大事なのは、
「自分はこういうミスをするんだ」
と意識することです。
この繰り返しがミスを少なくする1番の近道です。
(2)は連立方程式の問題です。
おそらくC問題を受験する人なら余裕で解いてほしいところです。
AやB問題を受験する人だと
どうやって解くの?ってなっている人が割と多いです。
解いたことがないってことはないはずです。
しかし、このタイプの問題に出会う回数はかなり少ないはずです。
ここで解けるかどうかの差は
どれだけ繰り返し復習をしたか
だと思います。
ぜひ、簡単に解ける人になるためにしっかし復習をしましょう!
(3)解説「計算問題」☆☆

このタイプはいきなり代入して計算しないようにしましょう!
いきなり代入しても答えは出ますが
計算量が増える場合がほとんどなのでおすすめしません。
より上を目指したい人は
単に解けることに満足するのではなく
どうやったらより簡単に速く解けるか
を意識するようにしてほしいです。
(4)解説「一次関数」☆☆

このタイプの問題は以前も出ていましたね。
かなり内容は簡単になりましたが。
今後もこのタイプの問題は出題される可能性は高いので
しっかり解けるようにしておきましょう。
(5)解説「確率」☆☆

去年までに比べて、確率はかなり解きやすくなりましたね。
ただ、標準レベルの学校のワークや塾のワークだとあまり載っていないタイプですね。
初見だと少し難しく感じると思います。
少し難しく感じる人は、
全国の入試問題を解いていろんな問題に慣れた方が良いですね!
下にリンクを貼っておくので、必要だと思う方は買って対策しましょう。
※上位校を受験する多くの人が使っている問題集です。
(6)解説「相対度数」☆☆

相対度数と方程式を絡めた問題はあまり多くないので、
もしかしたら少し苦戦した人がいたかもしれませんね。
しかし、内容的に難しくありません。
相対度数の求め方がしっかり分かっていれば解けたはずです。
もし分からなかった人は、次は解けるように復習をしておきましょう。
(7)解説「整数問題」☆☆☆

この問題も最近よく見かけますね。
公式を覚えていれば解けるような問題ではなく、
自分でしっかり考えて解いていく問題です。
C問題採用校を受験予定の人は、
普段から難しい問題でもしっかり考えて解くようにしましょう!
(8)解説「関数と図形(座標)」☆☆☆
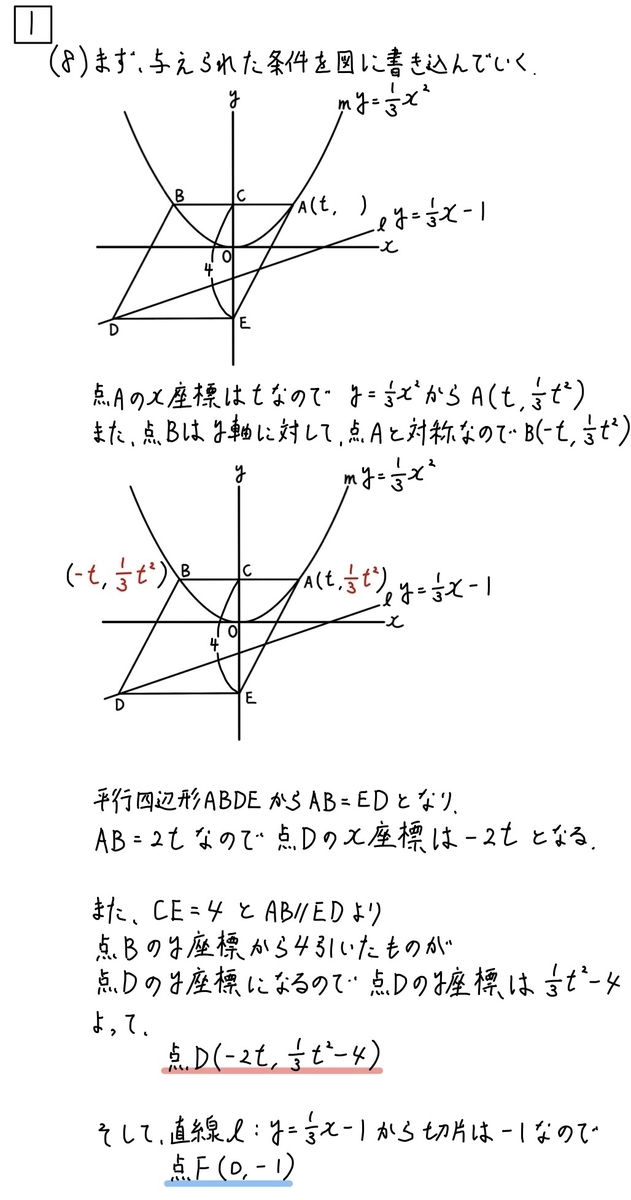

この問題は毎年出ていますね。
この問題で大事なのは
わかるところをグラフにどんどん書き込むことです。
眺めているだけで分からないという人がいますが
それは当たり前です。
しっかり書き込みながら
解いていくことを意識して解くようにしましょう!
第二問
(1)解説「平面図形(円の面積)」☆☆

これは落とせませんね。
ただ、上の解説にも書きましたが
πのつけ忘れがないように注意してくださいね!
(2)解説「相似の証明問題」☆☆

これは比較的やさしい証明問題でしたね。
できれば確実に正解したいところです。
証明問題が苦手な人は、
解説の真似をするところから始めましょう。
簡単な証明問題ならできるけど、難しい問題になるとできなくなる人も同様です。
証明問題のパターンはそこまで多くありません。
よっぽどの難問でない限り、見たことがない問題はないはずです。
今までに出会ってきた問題を全て解けるようにしておきましょう。
(3)①解説「平面図形(辺の長さ)」☆☆

先ほど証明した相似を利用して解く問題ですね。
これはよくある流れです。
比較的気付きやすい問題なので
この問題を落としていると周りと差が生まれる可能性があります。
数学が苦手であってもこの問題は正解したいところです。
(3)②解説「平面図形(面積)」☆☆☆



この問題は少し難易度が高いです。
この問題を解くためには
新しく相似の三角形を見つける必要があります。
その相似は、三角形ABCと三角形FEGです。
(三角形COGと三角形FEGでも解けますが、少し手順が増えます)
このような問題を解けるようになるのはなかなか難しいかもしれません。
ただ、何を見つければ解けるのかを意識し
似たような問題を繰り返し解いていくと
少しずつできるようになっていくはずです。
諦めずに最後まで取り組みましょう!
大阪では、平面図形と空間図形の問題が毎年出ます。
高得点を取るための対策をしたい人は下のような図形に特化した問題集がおすすめです!
第三問
(1)①解説「空間図形(面積)」☆☆

これは確実に正解したい問題ですね。
二等辺三角形や正三角形の面積を求める問題は
見た瞬間に解き方が思い浮かぶレベルにしておきましょう。
このような問題を落としているようではC問題採用校に合格するのはかなり厳しいと思います。
(1)②解説「空間図形(辺の長さ)」☆☆


この問題は比較的気付きやすい問題と思ったので☆2個にしています。
個人的にできれば解いてほしい問題です。
過去B問題に似たような問題が出題されています。
数学が苦手な人からすると難しく感じるかもしれませんが、
B問題にでも出題されるレベルなので頑張って解けるようにしていきましょう!
(1)③解説「空間図形(辺の長さ)」☆☆☆


これは補助線を引く必要がある問題でした。
僕がこの補助線を引くために意識したのは
DI:IEの比を求めるために相似の三角形がないかな
ということです。
このように答えを求めるために何が必要であるのか
を考えましょう。
ここを意識して数学を解くようにしないと数学は得意になることはないと思います。
天才的な数学のセンスを持っている人除いて笑
(2)①解説「空間図形(辺の長さ)」☆☆
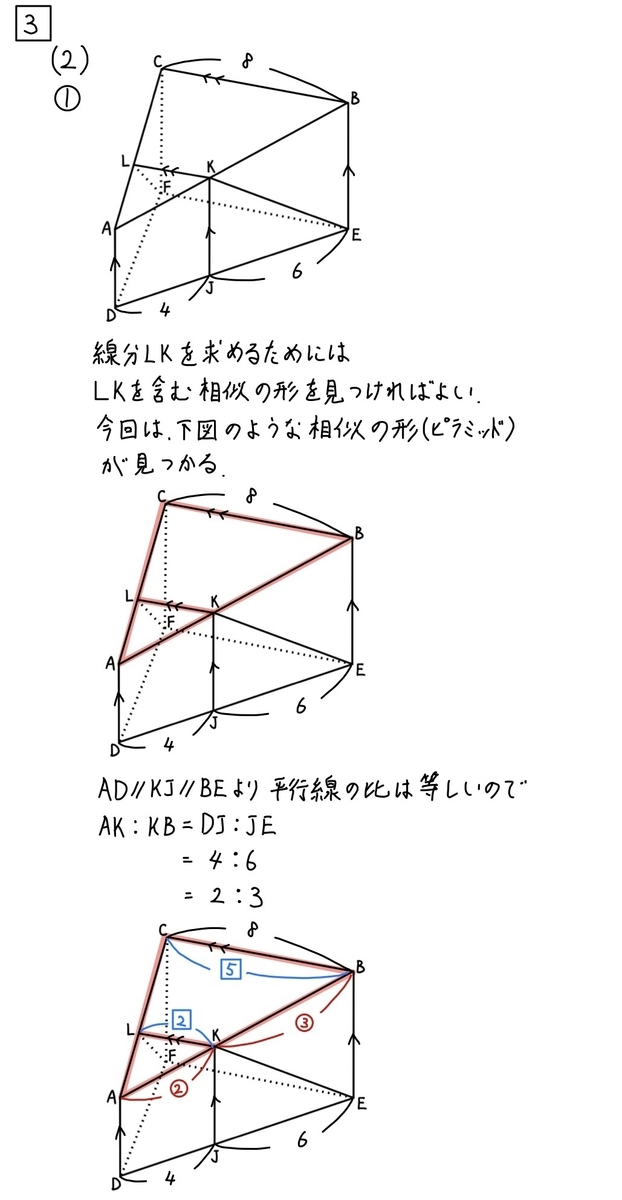

これは非常に解きやすかったですね。
これは落としたくない問題です。
この問題を難しく感じた人は
相似が絡んだ問題を集中的に解いてみましょう。
(2)②解説「空間図形(体積)」☆☆☆

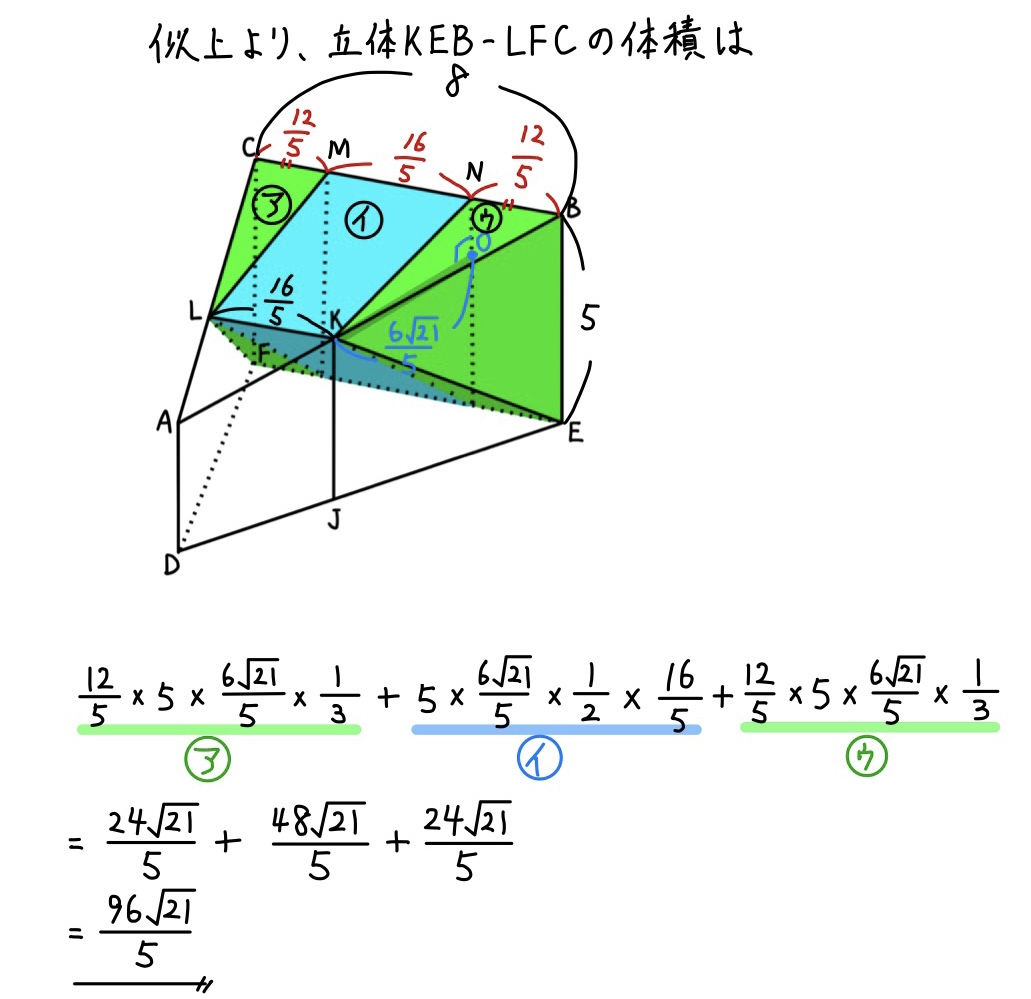
上の解説を見ると
そこまで難しく感じないかもしれませんね。
ただ、求める体積を分割するのは思いつくかもしれませんが
相似を利用して高さを求めるところが結構難しかったと個人的に思います。
この高さは上の解説でいうKOのところですね。
このKOがJPと同じ長さであることが分かれば、解くことができたでしょう。
まあ時間的なことを考慮すると、
この問題はできなくてもいいかなと思います。
総括
図形以外の分野において、
去年はよく見る問題が多かったですが、今年は考える問題が増えましたね。
1つ1つはそこまで難しくないですが、時間をかけ過ぎると後半の図形問題がしんどくなります。
図形問題において、
図形問題だけで見ると、若干簡単になったと思います。
「数学が得意な人」と「数学がそこそこ得意な人」だと差はあまりつかなかったのではないでしょうか。
全体的に見ると、バランスが取れた難易度に落ち着いた印象です。
もう少し図形問題は難しくしてもいい気はしますが、今後この難易度が続くといいなと個人的に思いました。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
上位校を目指す人へおすすめの問題集
2021年に行われた全国の入試問題が収録された問題集です。
特に上位校を目指す人は必ず解いている!
と言っていいものになります。
意欲がある人はぜひ購入しどんどんチャレンジしましょう!
今回は2022年大阪府公立高校入試数学C問題をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。