
公開日2022/03/13
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
自分の勉強のために解説を書いています。
間違い等あればお気軽に指摘してくれると嬉しいです。
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
解説している問題は発表されるまでお待ちください。
第一問
(1)〜(5)解説「計算問題」☆

どの高校を受験するにしても、これらの問題は確実に正解したいところです。
特に(1)、(2)、(4)は符号のミスが起きやすい問題です。
毎年、似たような問題が出題されるので
これらの問題でミスが多い人は要注意です。
また、(4)、(5)のような展開の問題において
B問題を採用されている高校を受験するなら
間違いなく展開の公式は覚えておくべきです。
おそらく合格者の中にも
覚えている人と覚えていない人が混在している状況になると思いますが
覚えていない人は
間違いなく高校の数学の最初からつまづくでしょう。
そうなりたくなければ、しっかり覚えておいてくださいね!
第二問
(1)解説「方程式」☆(2)「解の公式」☆

(1)は解けましたか?
久しぶりにこのような問題をやると、どんな答えを書くのか忘れている人が毎年います。
やはり、定期的に基本的な問題は復習するようにしてくださいね。
(2)は意外とできる人が多いイメージです。
ただ、符号のミスが非常に出やすい問題なので
日頃からミスをしないように演習することを心掛けましょう!
(3)解説「資料の活用」☆☆

数学が苦手な人は、このような問題を見ると
一瞬で難しそうと判断して解くことすら放棄する人が割といます。
この習慣は、小学校から続いているはずなので
小学校のときから最低1分は考える癖をつけておいてほしいですね。
この問題は、平均値、最頻値、中央値を求める問題ですが
1つ1つは難しい問題ではありません。
必ずできる問題なので、あきらめずに頑張ってください。
(4)解説「確率」☆☆(5)「連続する整数(方程式)」☆☆

(4)のようなカードやトランプのような問題は、表で解くべきことをおすすめします。
数え忘れが起こりにくい上に、応用がききます。
入試はいかにミスをしないかが非常に大事です。
自分にとってミスの少ないやり方を選択するようにしましょう。
特にミスが多い人は、どんなミスが多いのか自覚することから始めましょう。
(5)は非常にシンプルな問題ですね。
連続する3つの整数をa、a+1、a+2のように表すことさえできれば解けたはずです。
これを思いつかなければ、勉強不足と言わざるを得ません。
なぜなら、学校や塾のワークで必ず載っているような問題だからです。
ただ、今回解けなくても次に生かしましょう。
できなかったことをできるようにするのが勉強です。
これは数学だけでなく、生きていく上で全てにおいて言えることです。
(6)解説「円周角」☆☆

これは少し難しめの問題でしたね。
このような問題が苦手な人はサッと飛ばすのもありかなと思います。
ただ、できれば上の解説のような解き方はサクッと思いついてほしい問題ではあります。
偏差値55以上の学校を受験するなら確実にできておくべき問題ですね。
(7)解説「平方根」☆☆

このタイプの問題は最近ちょこちょこ見ますね。
数年前に、大阪でも似たような問題が出題されていました。
その問題を数学が苦手な生徒が解いているのを見ていると、
まず、何をすればいいのか分かっていない様子でしたね。
だから、手が完全に止まっていました。
ただ、こういった問題は最初何をすればいいのか分からなくてもいいのです。
手を動かして調べていく作業が非常に大事です。
これをしないと、どんな問題も決してできるようにはなりません。
間違ったことをしていても構わないので
しっかり手を動かして考える癖をつけましょう!
(8)解説「関数(座標)」☆☆☆


この問題は、数学が苦手なら飛ばしてもいいんじゃないかなと思います。
ただ、偏差値50以上の高校を目指す人は必ず解けるようにしておきましょう。
1つ1つは難しいことはないのですが、答えに辿り着くまでの手順が少し多いです。
ここで大事になってくるのは、
答えを求めるために、次に何をすればいいのかを常に考えることです。
これを常に考えるように意識するだけで、徐々に数学はできるようになっていきます。
最初はなかなか思いつかないと思いますが、焦らず続けていきましょう。
第三問
(1)①-③解説「関数(規則性・連立方程式)」☆☆

これは毎年の定番の問題です。
ここは確実に全部正解しましょう。
正直、ここを落としていては偏差値50以上の学校に合格するのはかなり難しいです。
もし偏差値50以上を狙っていて、この問題ができない状態なのであれば
勉強量をもっと増やさないとダメです。
僕の教え子たちには、どんな学校を受験するにしてもここは満点を取らせるようにします。
(2)解説「関数(連立方程式)」☆☆

この問題は(1)②ができていれば、意外と出来ちゃう問題です。
ただ、問題文が少し長いので最初からあきらめちゃう人が一定数いますね。
でも、、これって逆にチャンスですよね。
周りが諦める問題を確実にできるようにすれば、一歩リードできる訳です。
頑張ってくださいね!
第四問
[Ⅰ](1)解説「相似証明」☆☆

今年の相似の証明問題は簡単でしたね。
「2組の角がそれぞれ等しい」の条件のときは
確実に正解したいところです。
証明問題が苦手な人は、
まず与えられた情報を図に書きこまない人が非常に多いです。
少しでもできるようになりたい人は、
ぜひ図に書きこんでみてください!
ここで行動に移すことができる素直な人が合格する人です。
あなたはどっちですか?
[Ⅰ](2)①解説「平面図形(辺の長さ)」☆☆
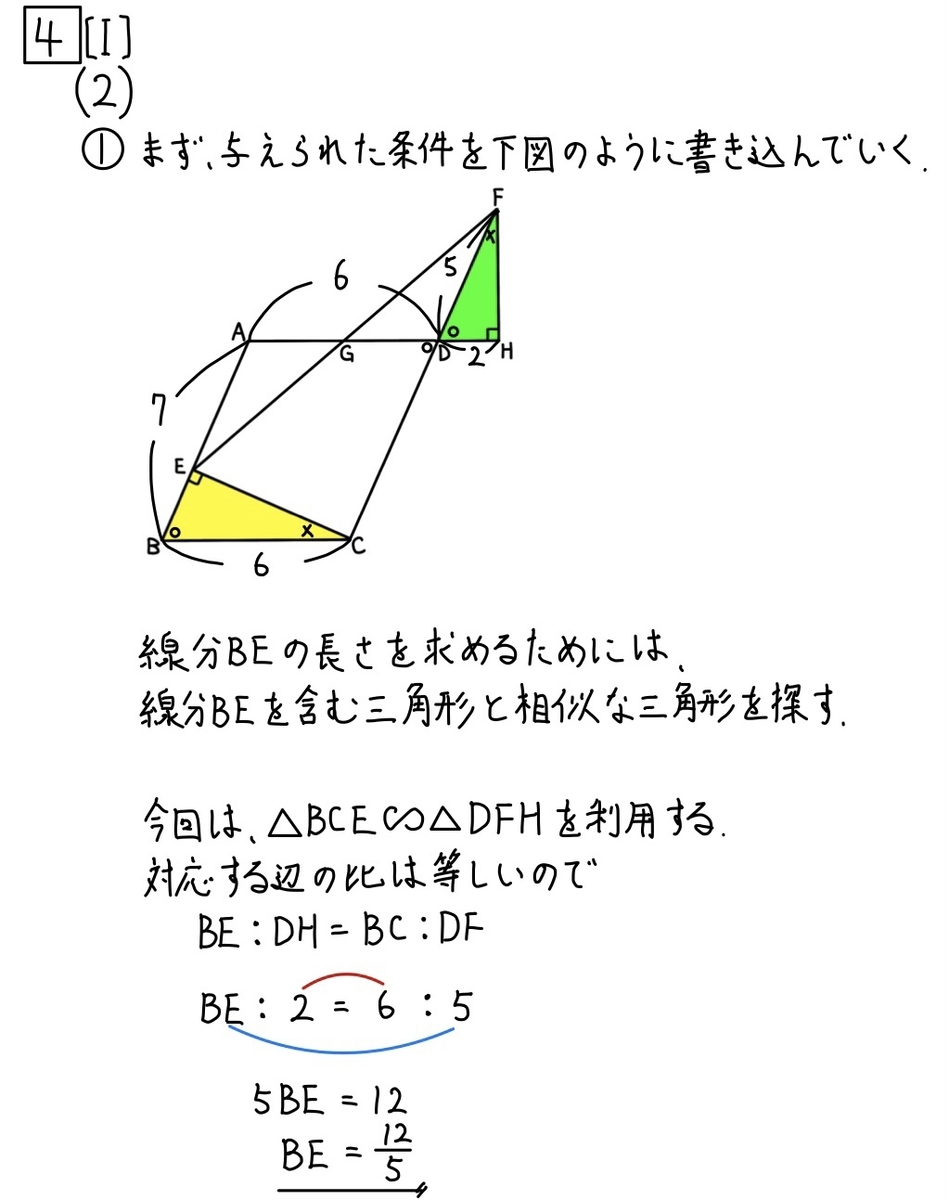
この問題は(1)で証明した相似を使って解くだけでした。
だから、できた人は結構多かったのではないかなと思います。
B問題採用校の中で上位の学校を受験した人は、
確実に正解したい問題ですね。
[Ⅰ](2)②解説「平面図形(面積)」☆☆☆



これは上位校を受験する人はぜひともできるようになってほしい問題です。
三角形FGDの面積を求めるためには
GDとFHの長さを求める必要がありました。
FHは三平方の定理を使うだけなので簡単でしたが、
GDを求めるのは少し難しかったですね。
ただ、このGDを求めるために何をすればいいのかが分かっていれば、そこまで難しくなかったかと思います。
でも、この部分って意外と教えてもらえない部分なんですよね。
こうやったら解けるよって教えてもらっても、なんでその解き方をするのかは教えてもらえません。
だから、この問題ができたとしても、似たような他の問題ではできないんですよね。
このような悩みを抱えている人は結構いると思います。
そういった人は、ぜひ教えてもらっている先生に次のような質問をしてみてください。
「この解き方をすれば解けるのは分かったんですけど、何でこの解き方をするのですか」と。
[Ⅱ](3)解説「ねじれの位置」☆

大阪の作問している方は、ねじれの位置が好きですね笑笑
ここ数年で、3回目だった気がします笑
まあ、出来があんまり良くないから出題されるのだと思いますけどね。
このような問題は確実に解けるようになってほしいですが、
「ねじれの位置って何?」
って聞かれたら答えられますか?
問題は解けるけど、答えられない人は
ぜひ答えられるようにしておきましょう!
[Ⅱ](4)①解説「空間図形(辺の長さ)」☆☆

この問題は出来ましたか?
これは確実に解いてほしい問題でした。
なぜなら、学校や塾の問題集に間違いなく載っている問題だからです。
ただ、この問題を公式のように解かせようとしてたりするんですよね。
だから、何も考えずに
(3+7)÷2=5
としちゃってる人が必ずいるんですよね。
これは中点なら正解になるんですけど。
とりあえず、この問題ができなかった人は
学校の問題集(中3)で探してみてください。
もし問題集のどの問題と同じか分からなければ、学校の先生に聞いてみてください。
[Ⅱ](4)②解説「空間図形(体積)」☆☆☆


この問題は一見そこまで難しそうに見えませんが
意外と出来が悪いような気がします。
上の解説では、
さらっと三角形BIJを底面にすると書きましたが
これが分からない人が結構いるんじゃないかなと個人的に思います。
そして、仮に三角形BIJが底面だと分かったとしても
高さをFBだと分からない人も多いような気がします。
図的にFIが高さに見えちゃうような気がするんですよね。
さらに、三角形BIJの面積を求めることも意外と難しいんですよね。
三平方の定理と相似を使って解く必要があるので。
ただ、これは上位校を受験するのであれば確実にできるようになってほしい問題です。
C問題採用校を受験するような人は、ぜひできるようにしておきましょう!
総括
去年と同じくらいの難易度だったのではないかなと思います。
ただ、人によっては解きにくいと感じるかもしれない問題もあったので、難しくなったと感じる人がいたでしょう。
このことを考慮しても、ほんの少しだけ難しくなった程度でほぼ去年と同じ難易度で問題ないかなと思います。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
上位校を目指す人へおすすめの問題集
2021年に行われた全国の入試問題が収録された問題集です。
特に上位校を目指す人は必ず解いている!
と言っていいものになります。
意欲がある人はぜひ購入しどんどんチャレンジしましょう!
今回は2022年大阪府公立高校入試数学B問題をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。