
公開日2020/09/15
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題をネット上で見つけることができませんでした。
掲載場所を知っている方がいれば、教えてほしいです。
第一問
1解説「計算問題」☆

難しい計算ではないですが、比較的ミスが出やすい問題が集まっています。
丁寧に確実に正解できるようにしましょう。
しかし、ミスは出るものです。
でも、ミスはあらかじめ防ぐことは可能だと僕は思っています。
その方法は、
自分がどんなミスが多いのか理解すること。
これがしっかり分かっていれば、
絶対に大きな失敗はしないです。
今からでも遅くはありません。
本番までにしっかりミスを意識しておきましょう。
2解説「解の公式」☆

解を求める問題は、
式をどんどん展開し、文字や数字を全部左側に移しましょう!
そして、因数分解できそうなら因数分解やって
難しそうなら、解の公式を使いましょう!
この問題は、確実に正解しなければなりません。
もしこの問題を見た瞬間難しいと思う人は
おそらく展開の公式をすら覚えていない可能性があります。
まず、そちらから勉強し直しましょう。
3解説「確率」☆
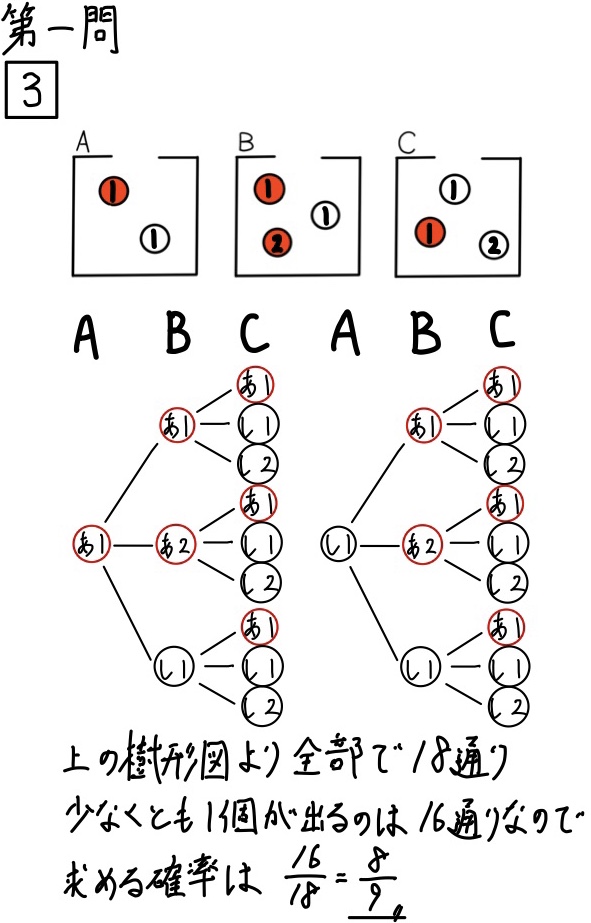
この問題は、樹形図をしっかり書いて考えてみましょう!
そして、赤玉や白玉に名前(上の画像だと、あ1、あ2、し1、し2のように)をつけてあげると解きやすくなると思います。
「少なくとも〜」ってあれば、工夫して解くとはやく解ける場合があります。
数学が得意な人は、工夫して解けると良いですね!
その工夫は、自分で考えてみましょう。
もしわからなければ、先生に聞きにいってくださいね!
また、数学がそこまで得意じゃないって人は
上のような解き方で問題ありません。
まず大事なことは、正解にたどり着くことですからね!
4解説「円錐の角度(孤の長さ)」☆

この問題は、上のように周の長さで判断するのが一番楽だと思います。
一見、展開してできる扇型の角度を求める問題のように見えますが
(これでも解けます)
周の長さで解くべきだと思います。
1つの解き方にこだわるのではなく
いろんな解き方をできれば身につけて欲しいです。
しかし、数学が苦手な人の場合、
まず、1つの解き方を完璧に身につくまで繰り返しましょう。
苦手だと感じている人のほとんどは、反復回数が少ないことが原因です。
2、3回で簡単に身につくなんて考えるべきじゃないです。
もちろん、中にはできちゃう人もいます。
でも、そんな人はほんの一部です。
数学ができる多くの人は、何回やったか分からないくらい繰り返しています。
あなたもぜひそれくらい繰り返していきましょう!
5解説「資料の整理」☆☆
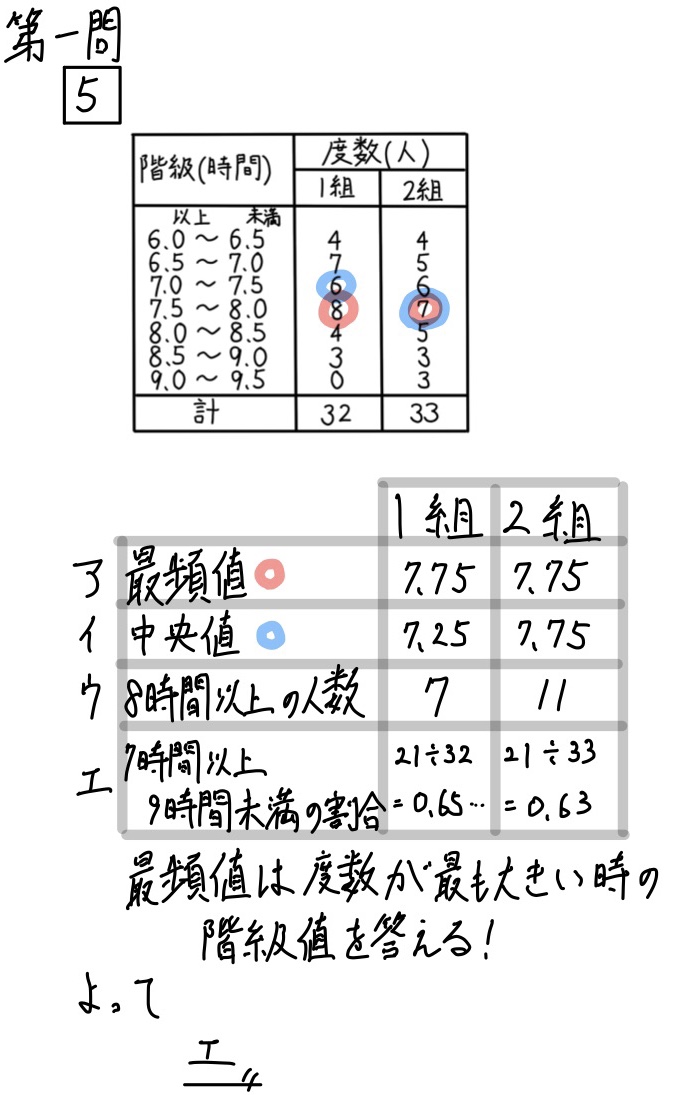
この問題は、1つ1つ丁寧に確認すること。
確認していく過程で、答えが分かったとしても全部確認するようにしましょう。
なぜなら計算ミスなどで間違っている可能性があるからです。
入試は確実に正解していくことを最優先しましょう。
だいたい同じレベルの人が同じ学校を受験します。
つまり、
一問の差、1点の差で合格と不合格が分かれるのです。
答えを早く出して、次の問題に早くいきたいのはものすごく分かります。
でも、他の人が正解する可能性が高い問題は落とせません。
このことをしっかり覚えておきましょう。
第二問
1(1)解説「変化の割合」☆
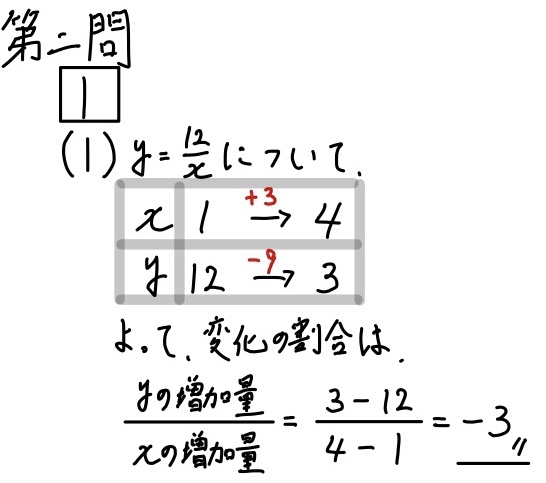
この問題は、塾のワークの基本問題で昨日中2の男の子に教えましたね。
つまり、確実に正解しないといけない問題ってことです。
変化の割合って何?って聞かれたら何て答えますか?
これをスラスラ答えられたら問題ありません。
もし黙っている状態なら、かなり危険かもしれません。
その状態ならいますぐに中2の教科書を確認しましょう。
1(2)解説「点と点の距離を求める問題」☆☆

これは点と点の距離を求める問題です。
この時に使う公式を思い浮かべることはできますか?
今回使うのは、
三平方の定理です。
まず、ここは必ず押さえておきましょう。
そして、三平方の定理を使うためには、
座標をしっかり求めておく必要があります。
ただ、グラフの問題なら
求めることができる座標は最初に求めておくのもいいですね。
そうすれば、問題をスムーズに解けると思います。
2解説「倍数の証明」☆☆

この問題は見たことありますよね?
そういう人は、学校の問題集で似たような問題を探してください。
見つけたら、次のことをしましょう。
問題文を読む。
解答を読む。
分からないところを質問する。
解答を覚える。
覚えたら、問題文を解く。
まあ、ごく当たり前のことを書いています笑
この中でも、覚えるというところを意識して取り組みましょう。
学校の問題集ができるようになった時、
また、この入試問題を解いてみてください。
きっと解けるようになっているはずです。
3解説「連立方程式の利用」☆☆

この問題は少しだけ難しくしてありますね。
まず、自分で文字を設定する必要があります。
しかも、単位付きで。
こういうのが少しあるだけで正答率が下がるんですよね。
また、足りない、余るタイプの連立方程式の利用は苦手な人が多い印象があります。
この問題も学校の問題集に載っているはずです。
ぜひ探して必ず解けるようにしておきましょう。
4解説「コンパスの作図」☆☆☆

問題文からどんな作図をすればいいのか分からなかった人が多かったかもしれませんね。
少し分かりにくい書き方になっていたので、
単に
垂直二等分線はこの書き方
角の二等分線は顔の書き方
のように書き方を暗記しているだけでは解けなかったと思います。
上の画像に少し分かりやすく言い換えてみました。
(赤のマーカーのところ)
この言い換えで分からなければ、
単に暗記しているだけになっているはずです。
そういう人は、
数学の先生に作図の書き方意外で覚えるべきところを教えてもらってくださいね。
4解説アニメーション「コンパスの作図」

✖︎印はコンパスの針を刺すところです。
第三問
解説アニメーション「図形の移動」

最初にこのアニメーションを見て解説を読むと分かりやすさが増すと思います。
1(1)解説「図形の移動」☆☆

この問題は、x=1、2、3…と続いていく時に
どんな風に移動していくのかが分かれば
解ける可能性がかなり高いです。
とりあえず、x=3の時に図形がどこにあるのかを
簡単な図
で構わないので描いてみましょう!
上の図は、説明するためにかなり丁寧に描いています。
あそこまで描く必要は全くありません。
大事なのは座標をしっかり考えながら描くことです。
(図形の移動だけど、点に注目しながら描くことが大事です)
座標の場所がしっかり分かっていれば、
図形が重なる部分の形がわかるはずです。
(今回、x=1〜6までは正方形になっていますね!)
これが分かれば面積を求めることはおまけみたいなものですよね。
1(2)解説「図形の移動(変域や式)」☆☆

まず、x=1〜10までの面積を具体的に求めた方が
動きの全体像が見えやすくなると思います。
(もちろん、書かなくてもわかる人はしなくても構いません)
面積を具体的に求めた画像見てください。(画像の一番上です)
すると、
x=0〜4までは増えていき
x=4〜6は一定で
x=6〜10までは減っていく
ことが分かりますね。
ここから、この3つの範囲に注目して式を立てていくことができますね。
式を立てていくのは上の画像にある図を見てもらえるとわかると思います。
1(2)解説「図形の移動(グラフ)」☆☆

表と式を求めることができていれば、
グラフは簡単に描くことができたでしょう。
二乗に比例する関数(x=0〜4)のグラフは
なめらかに描くことを意識して描きましょう。
たまに、ガタガタな人がいるので。
2解説「図形の移動(等しい面積)」☆☆☆
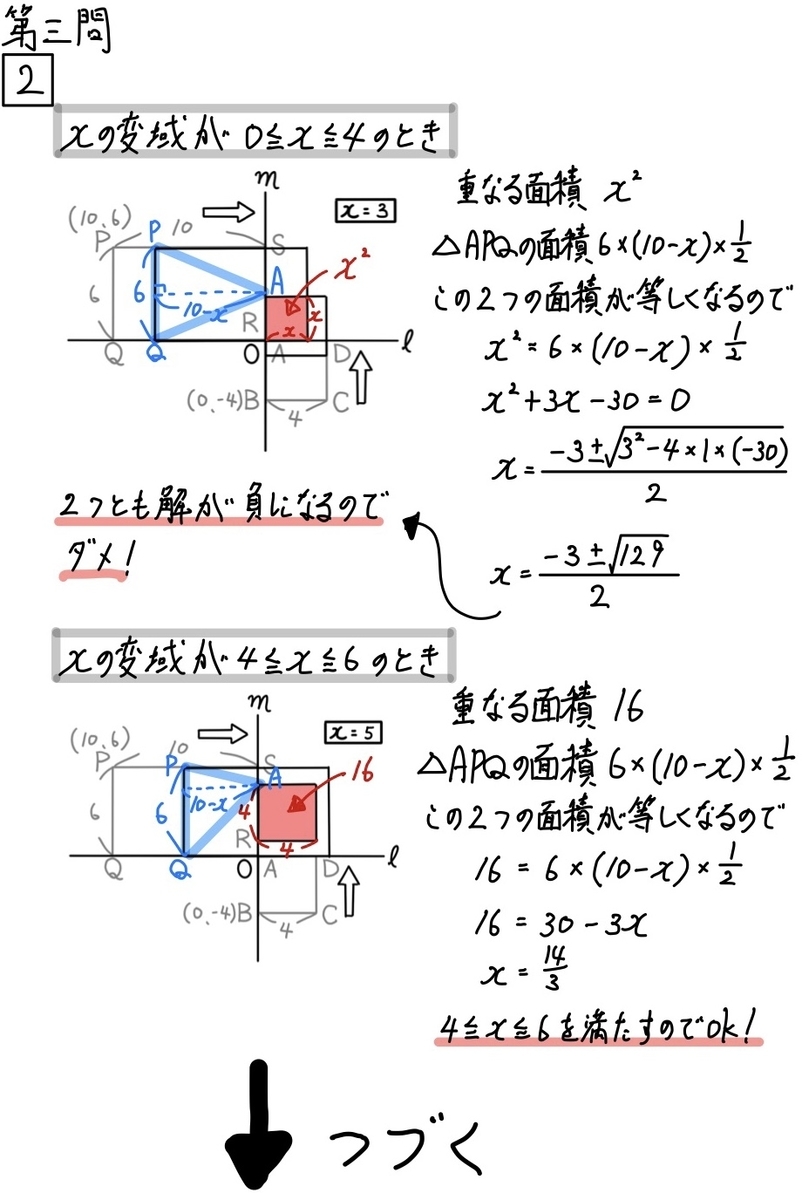

この問題は、各変域で面積が等しくなる部分を探す必要があります。
もし時間的に厳しい場合は飛ばしてもいいでしょう。
ただ、解説の量はかなり多く見えると思いますが、
やるべきことはそれほど多くありません。
難関校を受験予定の人はできるするべき問題ですね。
第四問
1解説「合同の証明」☆☆

少しだけ難易度が高い証明問題ですが、
偏差値50〜60くらいの学校を受験する人もできるようになってほしい問題ですね。
(めちゃくちゃ難しい問題ではありません)
円が絡んだ問題なので円周角を使うのは大丈夫だと思います。
しかし、二等辺三角形を見落としてしまう人は割といたかもしれませんね。
もし、途中で止まってしまったら何か見落としている情報がないか確認してみましょう。
意外と見落としで解けないことは多かったりするので。
2(1)解説「相似の利用」☆☆☆

円と二等辺三角形が絡むと、このような解き方をすることが多い印象ですね。
しかし、多くの人が苦手としている問題でしょう。
苦手というより、解く回数が極端に少ないから解けないだけな気もしますが。
僕自身も中学生の時、この問題は絶対に解けてなかったですね笑
そもそも、塾に行ってなかったので、勉強は苦手でしたが笑
まず、解き方を暗記して、この問題は絶対にできるようにしちゃいましょう。
そうするといつの間にかできるようになってます。
ちなみに、この問題は塾のワークに似たような問題が1問あったと思います。
応用問題のところに分類されていたと思います。
上位校を受験予定の人は、必ずできるようにしておきましょう!
2(2)解説「相似の利用」☆☆☆☆

正直に言いますね。
この問題解けませんでした笑
自分で長さを設定する問題は、苦手なんですよね。
っていうか、解き方の方針を完全に間違っていて解けませんでした笑
でも、次はもう解けますよ笑
この積み重ねで今の僕がありますから!
各都道府県のトップ校を受験予定の人はしっかりできるようにしておいた方がいいですね。
偏差値で言うと62、63あたりより下の場合、やらなくてもいいかもです。
数学が本当に得意!って人だけやればいいと思います。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年山形県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。