
公開日2021/12/4
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
自分の勉強のために解説を書いています。
間違い等あればお気軽に指摘してくれると嬉しいです。
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
問題→こちら
引用元:京都新聞HP
※引用元が京都になってますが、間違いではありません。
第一問
(1)~(6)解説「計算問題」☆
(1)93.4(2)88.6(3)82.2(4)80.2(5)77.6(6)83.4

ここの計算問題は基本的な問題ばかりなので
確実にすべて正解できるようにしておきましょう。
(7)解説「二乗に比例する関数」☆62.9%

この問題も基本的な問題ですね。
マイナスのつけ忘れなどをしないように
注意して計算しましょう。
(8)解説「確率」☆☆37.4%

この問題は難しくないですが、
素数を全てミスなく見つけることができなかった人が多かったのではないでしょうか。
もしこの問題で素数をうまく見つけることができなかった人は
1度でいいので100までの素数を探してみてください。
1度やっているかどうかの差は意外と大きいですよ。
(9)解説「平均値・最頻値」☆☆
(アイ)23.3(最頻値)35.1

この問題は決して難しくないですが
正解できる人が少ないイメージの問題です。
理由は、階級値を使った平均値の求め方を忘れている人が多いからです。
この求め方が分からないと、
ドミノ式に次の問題も解くことができないので
他の人と点差が広がっていくことになります。
このようなことがないように
この問題に限らず
基本的な求め方に穴がないようにしておきましょう!
第二問
(1)解説「直径の長さ」☆☆32.1%

この問題で大事なことは
「答えを出すために、何をすればならないか」
を考えることです。
この問題では円の直径を求める必要があります。
ここで考えなければならないのは、
「何が分かれば円の直径を求めることができるのか」
です。
その答えは、円周です。
そして、この円周を求めるために
次に何をしなければならないのかを考えましょう。
これを繰り返していけば、解けるはずです。
これは数学に限らず全ての科目で言えることです。
ぜひ他の科目でも意識して勉強してみてください。
(2)解説「コンパスを使った作図」☆☆☆10.6%

この作図は難しめでしたね。
実際、正答率もかなり低いですしね。
この問題は問題文をしっかり読んで
点Pがどの位置にくるかをしっかり把握できるかが鍵だったと思います。
これが分かれば、
角の二等分線、垂直二等分線
をそれぞれ描けばいいことが分かったはずです。
作図の問題で注意してほしいことは
「なんでこの作図の仕方をするのか」
をしっかり意識することです。
ぜひ普段から心掛けてみてください。
下に作図のアニメーションがあるので
ぜひ参考にしてくださいね!
(2)解説「コンパスを使った作図」アニメーション

(3)解説「最短距離」☆☆12.7%

この問題は定番ですね。
ただ、問題集では1、2問くらいしかないので演習不足かもしれません。
最短距離の問題は、
展開して考えるの
は鉄則です。
展開して考えることさえ分かれば
もっと多くの人が正解したはずです。
あとは上の解説のように解いていくだけです。
ぜひ覚えておいてくださいね!
(4)解説「最短距離」☆☆☆0.7%


この問題は(3)の応用問題ですね。
しかし、考え方は何も変わりません。
最短距離は展開して考えましょう。
ただ、上のようにおうぎ形を並べて考えるのが難しかったですね。
これは似たような問題を解いた経験があれば解けたかと思います。
もし似たような問題が解きたければ
学校か塾の先生に聞いてみてください。
もしくは、本屋さんで問題集を見てみましょう。
数学は、いろんな問題を解くことが大きなアドバンテージになります。
ぜひ数学が得意な人はたくさんの入試問題を解いてみてくださいね。
個人的には下のような問題集をおすすめしています。
※数えてみたらこの問題集には最短距離を求める問題が13問ほどありました。
第三問
(1)解説「線分の長さ(三平方の定理)・角度(円周角)」☆☆32.6%

この問題は難しくありません。
しかし、正解率はそこまで高くありません。
では、どのような人が正解できたのでしょうか。
それは
「自分で図を描いて考えた人」
です。
※一部の天才的な数学のセンスを持っている人は描かなくても解けちゃいますけどね笑
僕は普段指導している生徒には
図解の問題は手を動かしてどんどん書き込むように伝えています。
なぜならこの入試問題のようなタイプで解けなくなるからです。
何も手を動かさずに解けなかった人は
騙されたと思って問題文に書いてあることを図にしてみてください。
そうすれば、この問題はそこまで難しくなかったとわかるはずです。
(2)解説「角の二等分と垂直の証明」☆☆☆1.4%



この証明問題は難しかったですね
まず、何を証明したらいいのか分からなかった人が大半だったのではないでしょうか。
全く分からなかった人はこの問題を潔く捨てるべきでしたね。
解けないのに中途半端に時間を使うと、他の問題に影響が出ますからね。
考え方は上の解説に書いたのでぜひ参考にして頂ければなと思います。
あと、数学が苦手な人はこの問題は出来なくていいと個人的に思います。
それより、基本的な問題をしっかりできるようにしておきましょう。
(3)解説「線分の長さ」☆☆☆14%

この問題は解き方を教えてもらえれば
超簡単な問題だと思う人が多いのではないでしょうか。
ただ、この問題は個人的にかなり難しかったと思います。
何が難しかったのかというと、
「問題文に書いてあることを図にすること」
です。
(1)でも言いましたが
普段から図を描いて考えることは非常に大事です。
普段から図を描いて描く習慣があった人は
この問題もそこまで時間をかけずに解けたはずです。
もう一度言いますが、
普段から図を描いて解くようにしてくださいね!
図が描ければ、上の解説のように解けるはずです。
第四問
(1)解説「点の移動・図形の折り返し(変域)」☆☆36.7%

この問題以降の問題は非常に非常に難しかったです。
数学が苦手な人は解く必要がありませんので、
受験日までに他の問題をしっかりできるようにしておきましょう。
この問題は下のアニメーションを見て頂いて
上の解説を読むと理解できるはずです。
ぜひ見てくださいね。
(1)解説「点の移動・図形の折り返し(変域)」アニメーション
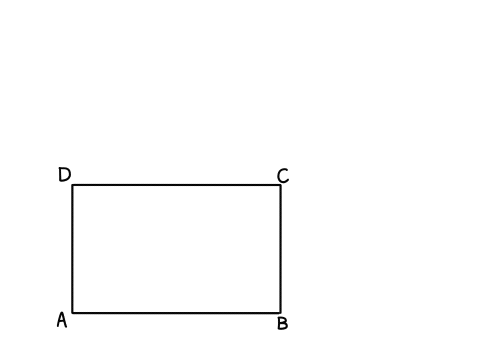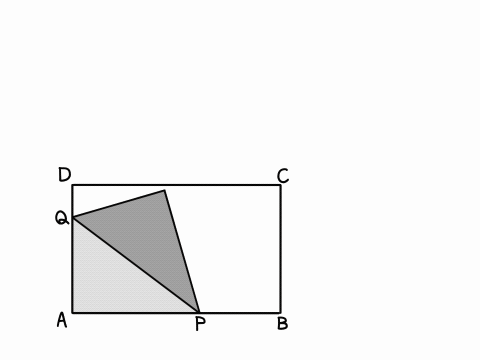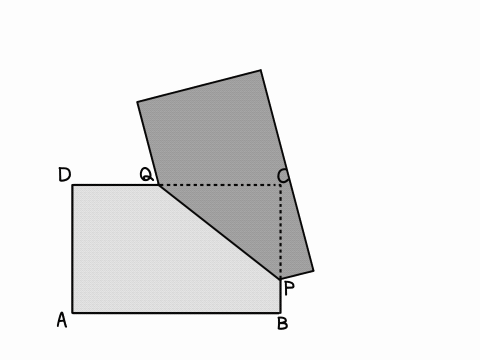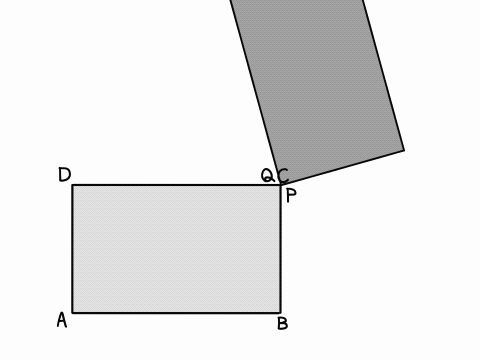
どこで灰色の形が変わっているのかに注目して見てくださいね!
(2)解説「点の移動・図形の折り返し(グラフ)」☆☆☆2.9%


この問題は大問3と同じように
自分で図が描けることが非常に大事です。
描けないと解くことができない問題でした。
そして、図が描けたとしても
台形の面積(8≦x≦10)をx、yを使って式に表すのは難しかったですね。
式を作らなくても解くことはできますが
なるべく式を考えてみてください。
一応、上の解説にはポイントになる図を描いているので
それを見ながらでいいのでチャレンジしてみましょう。
(3)解説「点の移動・図形の折り返し(移動した長さ)」☆☆☆0.4%



この問題は難し過ぎますね笑
答えも合ってるのか不安になる感じですしね笑
丁寧目に解説を書いたつもりなので
読んで頂ければわかるようになっているはずです。
もし読んで分からなければ、分からないままでも構いません。
この問題が解けなくても合否に全く影響が出ないような問題なので。
(4)解説「点の移動・図形の折り返し(移動した長さ)」☆☆☆☆0.1%

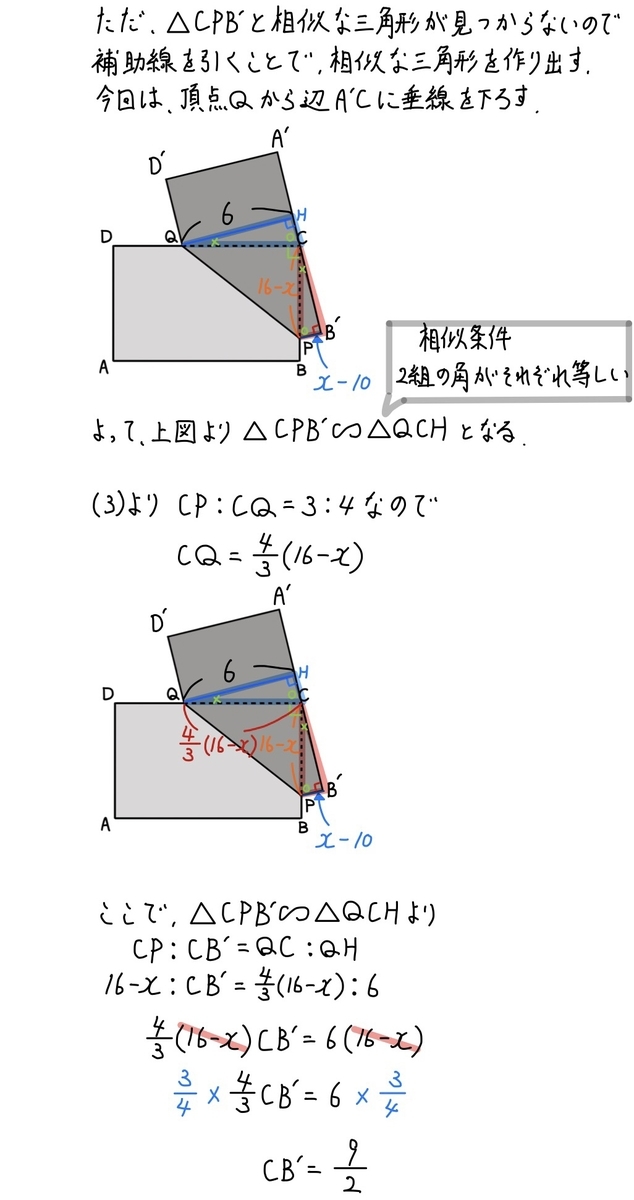

この問題は難し過ぎますね。
図を描くことが難しい上に
相似を使うための補助線を引く箇所も難しかったですね。
この問題は僕自身も制限時間内に解く自身は全くないです笑
このような問題をサラッと解けるような頭が欲しかったです笑
ただ、この問題は考え方は非常に大事な内容が詰まっていますので
しっかり理解するようにしておきましょう。
上位校の中の上位を目指す人は特に。
総括
難しい問題が非常に多く、数学で点差が開かない内容だったように感じました。
公立高校の入試問題なので、もっと標準的な問題が欲しかったですね。
2022年以降の受験生は、この年の問題ができなくても全く気にする必要はありません。
数学が特に得意でなければ、大問1、大問2のみしっかりできるようにしておきましょう。
ただ、上の解説で大事な考え方は書いてあります。
少しでも数学をできるようにしたいなっと思う人は
解説だけでも読んでみてください。
きっと何か得られるものはあるはずです。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
上位校を目指す人へおすすめの問題集
2021年に行われた全国の入試問題が収録された問題集です。
特に上位校を目指す人は必ず解いている!
と言っていいものになります。
意欲がある人はぜひ購入しどんどんチャレンジしましょう!
今回は2021年滋賀公立高校入試数学問題をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。