
公開日2020/04/25 更新日2020/12/01
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題はこちら
第一問
問1〜6解説「計算問題」☆

基本的な問題ばかりですね。
ただ、ミスをする可能性はあります。
なるべく途中式は書いてミスを見つけやすい状況にしておきましょう。
いろんな場所に計算が書いてあるような状況は絶対にダメです。
問7解説「文字式」☆問8「面積」☆☆

7番のような問題は具体的な数値で考えることをおすすめします。
やはり具体的な数値で考えた方が圧倒的にミスが減ります。
どうやればミスが減るのか常に意識しましょう。
8番は問題文で30度が書いてあるので、1:2:√3を使って解くことをすぐに思いつくようにして欲しいです。
また、円周角で60度が出てくると正三角形ができることも知っておいてほしいです。
あと、二等辺三角形にがよく出てくることも覚えておきましょう。
数学は与えられたヒントから次に何をすべきかを考えるような問題です。
だから、すぐに思い出せるような状態にしなければなりません。
では、どうすればすぐに思い出せるのか。
それは、多くの問題を解くことでしか身につきません。
ぜひ、たくさん入試問題を解いていきましょう。
第二問
問1(1)解説「文字式」☆(2)「方程式」☆☆

☆1つでもいいかなと思いましたが、自分で方程式を作らなければならないので☆☆にしました。
ただ、(2)を方程式を使って解くという発想に至らなかった人もいたかもしれませんね。
問題を解く考え方としては、
①何歳年上なのか知りたいのか
②じゃあ、3人がそれぞれ何歳なのか求めないとダメだな
③ということは、方程式を立てて考えないと!
のような流れですね。
しっかりできるようにしておきましょう!
問2(1)解説「場合の数」☆☆(2)「確率」☆☆
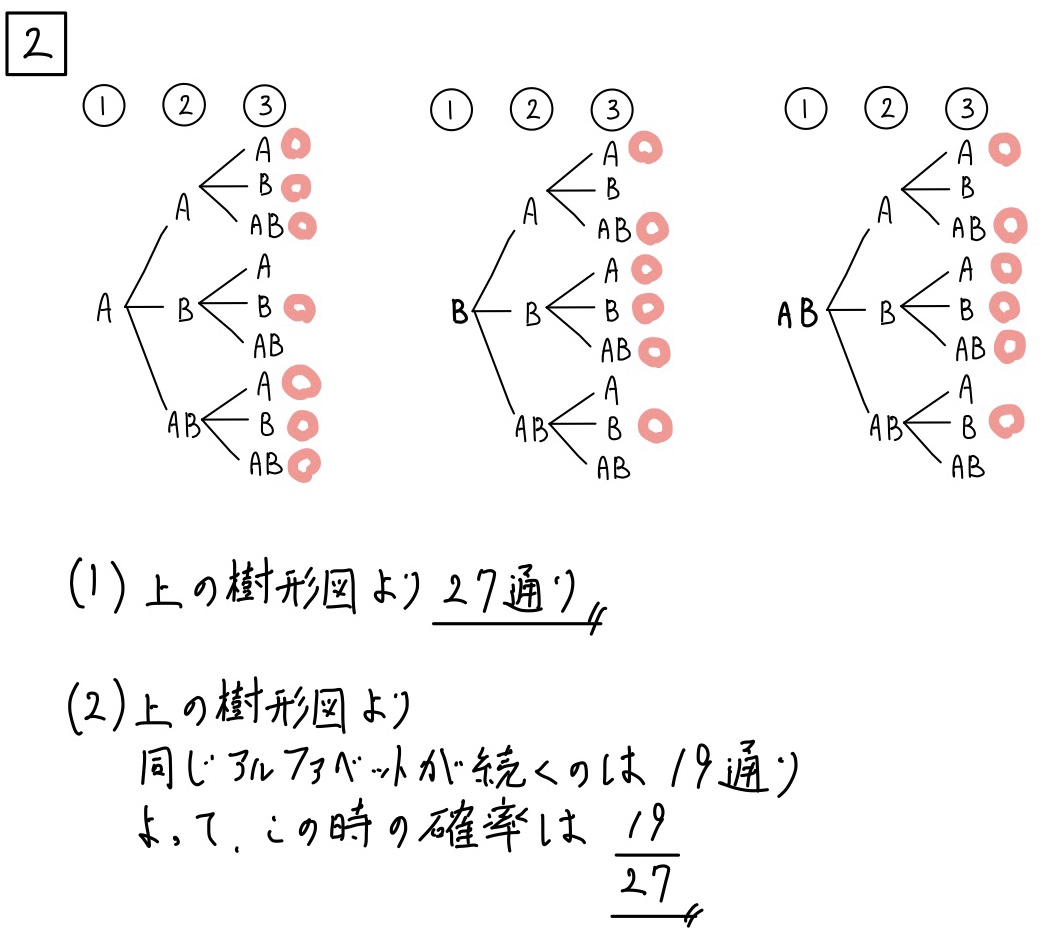
A、B、ABのようにABをまとめて考えるのは少し目新しいですね。
ただ、やることは変わりません。
上の解説のように樹形図を書いていきましょう。
樹形図を書くときは規則的に書くことがミスをしないポイントです。
そして、書くことさえ出来ればこの問題は必ず正解できちゃいますね。
問3(1)解説「直線の式」☆☆(2)「変域」☆☆
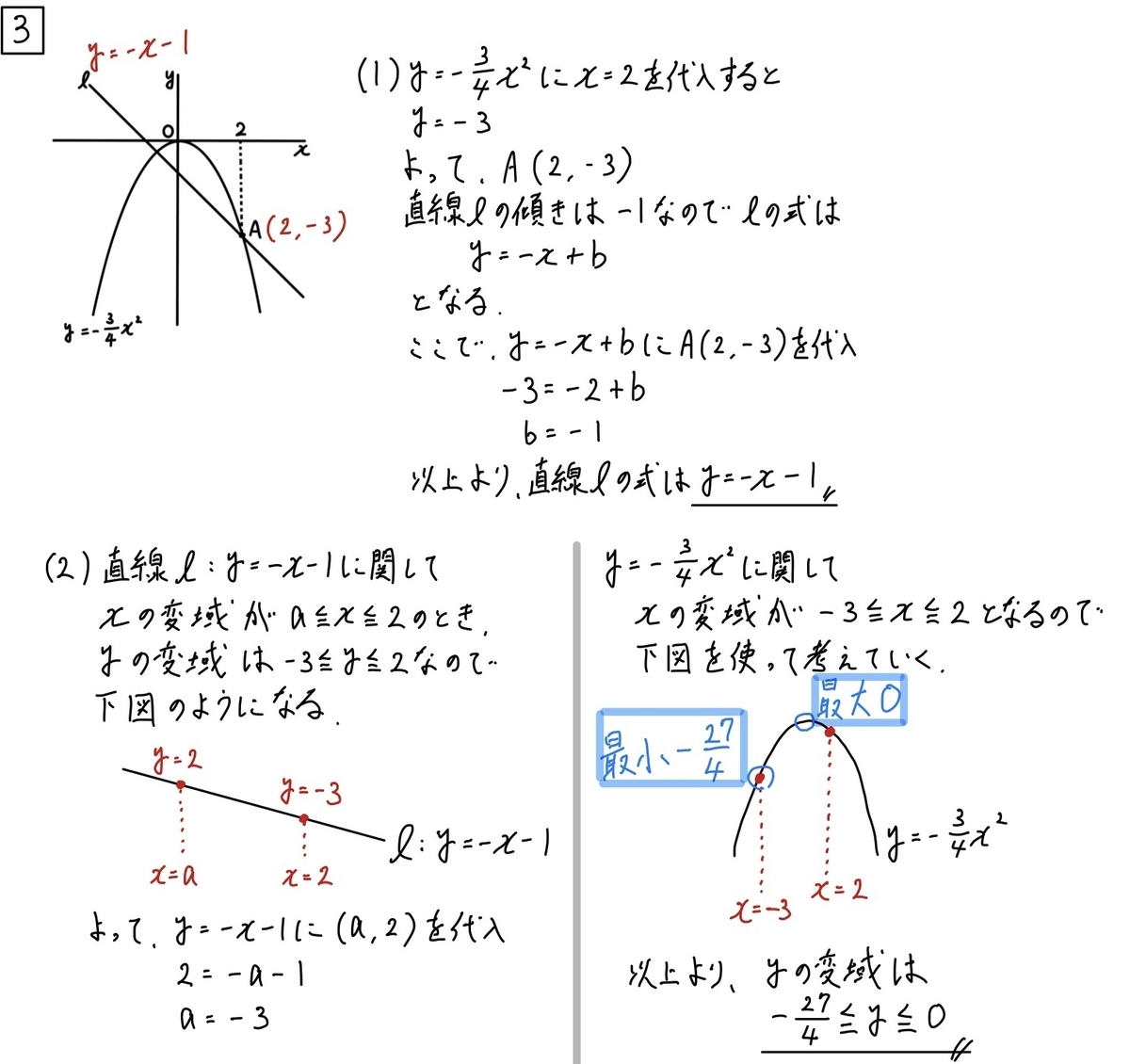
こういう問題になると、できなくなる人が急に増えてきますよね。
それはなぜなのか。
理由は簡単で、今まで機械的に解いてきたからです。
できるようになるために必要なのは、
この答えを求めるために、次に何をしたらいいのかを考えること
です。
数学が苦手な子に多くは、これを考えていません。
そして、考えるためには手を動かし続けなければならないのです。
具体的には、
問題文のヒントを図に書き込んだり、図がなければ図を書いたりすることです。
だから、手を動かしていない時点で考えてないのと同じなのです。
よくこんなことを言われます。
何を書けばいいのか分からないと。
ほんまに?っていつも言っちゃうんですが、それはありえないんですよね。
たとえば、座標が与えれていたとしましょう。
その座標を図に書き込んでごらんと言うとすぐ書き込んでくれます。
これが分からないの?難しい?ってなりますよね。
こんなことは思っていても言いませんが。
特にこの作業をしない人は(2)は全くできないと思います。
間違ってもいいので、何か図を書いてみましょう。
この一歩が大きな一歩になるのだから。
第三問
問1(1)解説「資料の整理(相対度数)」☆(2)「資料の整理(相対度数)」☆☆

(1)は定番の問題ですね。
どの学校を受験するにしてもできなければならない問題です。
(2)も内容的には(1)と同じです。
違うのは、説明する部分ですね。
こういう問題をできるように普段から練習するしかありません。
いきなりできないのは当然なので、全国の似たような問題を探してチャレンジしていきましょう。
問2(1)解説「読み取る問題」☆☆

この問題は中学受験で出てきそうな問題ですね。
正直、内容的には難しくないです。
ただ、できなかった人が多かったかもしれませんね。
普段から公式に当てはめるだけで解いてきた人は特に出来なかったと思います。
今後、このような問題はどんどん増えていきます。
しっかり図に書き込んで情報を整理していきましょう。
この問題の場合、どんどん分かっている距離をどんどん書き込んでいくと、2つの青の◯部分だけがわかない状態になります。
しかし、2つの青の◯部分の合計の長さわかります。
つまり、一つ分の長さがわかります。
ここまでできると、答えは出ちゃいますね。
問2(2)ア解説「読み取る問題(グラフ)」☆☆

この問題も苦戦する人が多いと思います。
グラフを書くには、距離、かかる時間、速さが分かっている必要があります。
しかし、この問題はすべて自分で調べたり計算したりする必要があります。
この作業をする問題は学校であまり解かないと思います。
なぜなら、1問にかなり時間がかかる上に、学力差があるクラスだと授業が成り立たないからです。
学校の授業の問題で特に困ることがなければ、全国の公立過去問でどんどん解いていくべきですね。
問2(2)イ解説「読み取る問題(連立方程式)」☆☆

これはかなり難しかったと思います。
まず、状況をしっかり理解している必要がある上に、計算がかなり複雑です。
制限時間のことを考えると、この問題は飛ばして他の問題が終わってからチャレンジした方が賢いと思います。
第四問
問1解説「辺の長さ(三平方の定理)」☆☆

この問題は、三平方の定理を使うだけですね。
あんまり良くはないですが、なぜ90度になるか分からなくても見た目から解けちゃう問題でもありました。
確実に正解しましょう。
問2(1)解説「台形の証明(定義)」☆☆

これはかなり珍しい問題でしたね。
ワークでほとんど見たことない問題です。
ただ、台形の定義は一応習います。
しかし、二等辺三角形や平行四辺形の証明がメインになりがちなので盲点を突かれた形になりましたね。
この機会に、しっかりおさえときましょう。
問2(2)解説「等高三角形(面積)」☆☆

一見、難しいように見えるかもしれません。
しかし、内容的には等高三角形の知識を使っただけです。
等高三角形の場合、底辺の比と面積の比が等しくなります。
これさえ気付けば簡単に解けたと思います。
問2(3)解説「等高三角形(面積)」☆☆☆☆
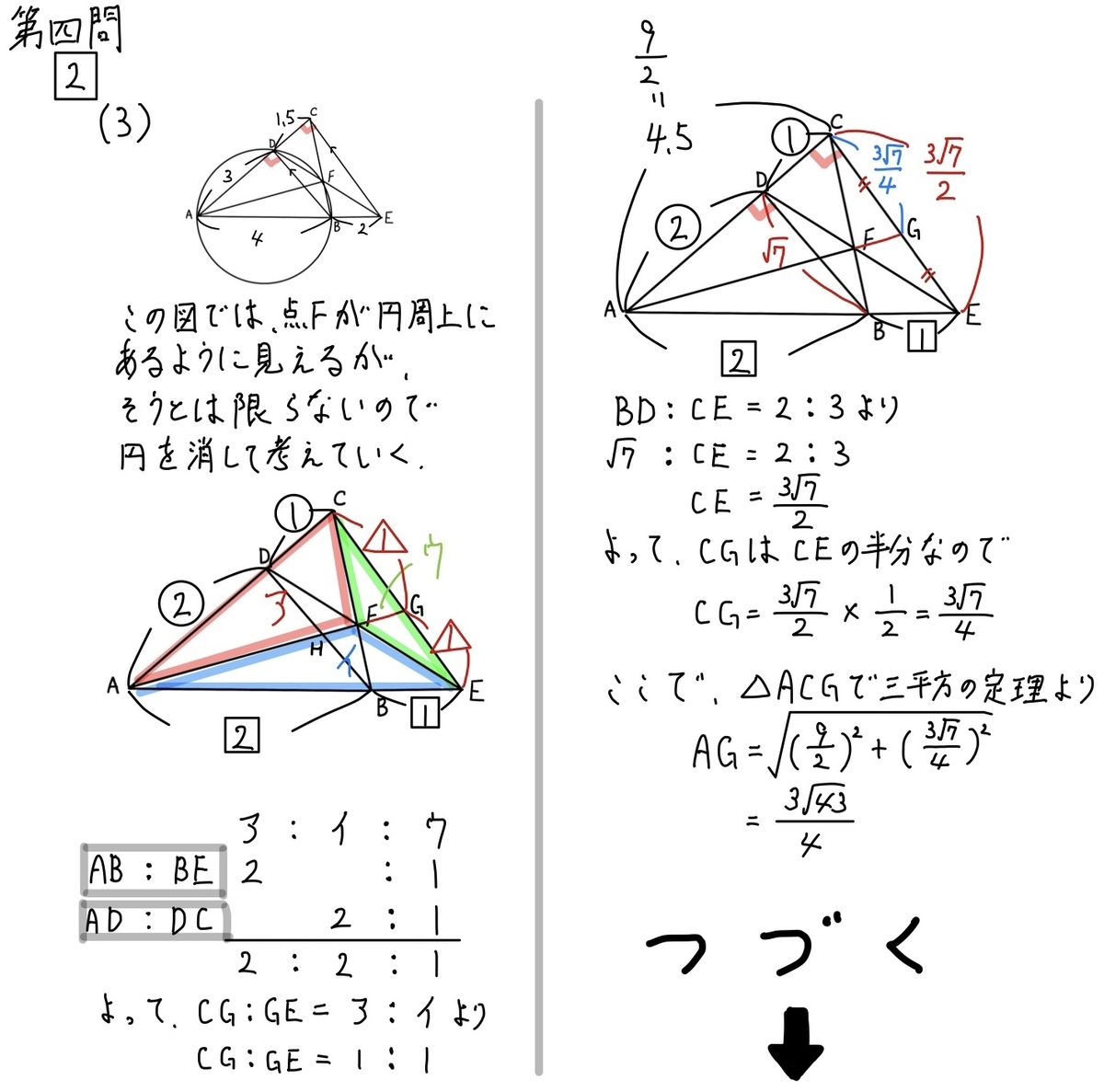
ここまでの流れはわかりました?
一応かなり丁寧に書いたつもりです。
もし分からなければこの問題は出来なくて構いません!
他の問題をできるようにした方が賢いです!

これは本当に激ムズでしたね笑
これが出来なくて不合格になる学校はありません。
そういう問題でした。
この問題を解く流れは
①AFを求めたい
②AGを求めて、AH:HF:FGの比が分かれば求められそう
③三角形AGFは直角三角形だから、CGがわかれば、AGを求められる
④CEの長さを求まるから、CG:GEが分かればCG求められる
という感じです。
あと、CG:GEを求めるためにチェバの定理(高校内容)を使うと楽だったかもしれません。
進学塾などでは習うかも。
上の解説では、チェバの定理は使いませんでした。
そこまで必要性を感じないので笑
でも、知っていて損はしませんよ!
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年宮城県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。