
公開日2020/05/02
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題を見たい方は下のリンクからどうぞ。
※下野新聞から引用
第一問
(1)〜(5)解説「計算問題」☆(6)〜(7)「方程式」☆☆

これらの問題はどこの学校を受験するにしてもできてほしい問題です。
いかにミスをしないかがカギなので、もしミスが多い人はどんな間違いが多いのかを必ず意識しましょう。
ここで、単に計算ミスで済まさないことが本当に大事です。
しょうもない足し算、引き算のミスもしっかり意識しましょう。
(8)解説「円周角」☆(9)「方程式」☆(10)「確率」☆

(8)は90度の角度に気付くのは大丈夫だと思います。
しかし、意外と二等辺三角形に気付かない人がいます。
こういう人は、確実に問題を解く量が少なすぎます。
すぐに問題集で円周角の問題を一通り解いていきましょう。
(9)(10)は基本的な問題で特にいうことはありません。
(11)解説「回転体(体積)」☆(12)「相似比」 ☆☆

ここもかなり基本的な問題ですね。
もし、このような問題でつまずいているのであれば、全国の公立入試問題の第1問だけ解きまくるといいと思います。
最初は同じレベルの問題が多いので。
ただ、たまに難しい問題もあるので、解説を見て絶対に無理だなと思う問題は飛ばしましょう。
(13)解説「一次関数」☆(14)「資料の整理」

(13)は傾き、切片についてしっかりわかっていれば問題ないです。
特に
傾きが正なら右上がり
傾きが負なら右下がり
になることは常に意識しましょう。
たまに無意識で間違っている人を見かけます。
(14)は資料の整理の問題ですね。
中3の最後に習うので、出来がイマイチな人がままで入試に挑む人も多いかもしれません。
ただ、内容的には小学生で習う比と同じです。
入試までにしっかりできるようにしておきましょう。
第二問
(1)解説「コンパスを使った作図」☆

この問題は回転させるなど書いていますが、ほぼ角の二等分線を引く問題ですね。
だから、しっかり読んでいれば難しくありません。
しっかり正解しちゃいましょう!
(1)解説「コンパスを使った作図」アニメーション
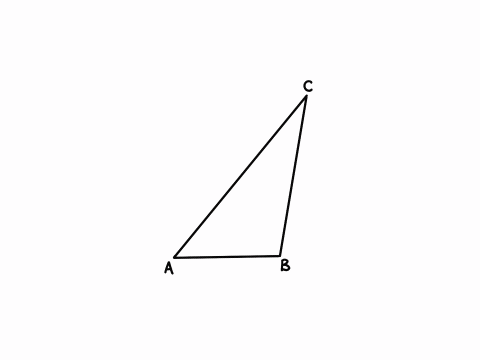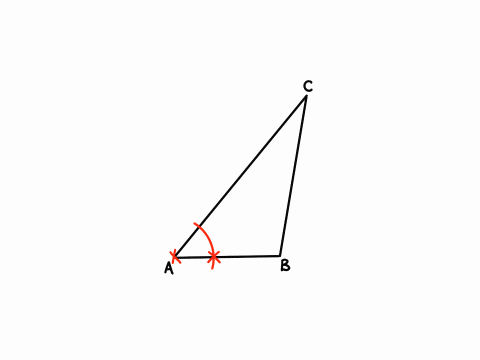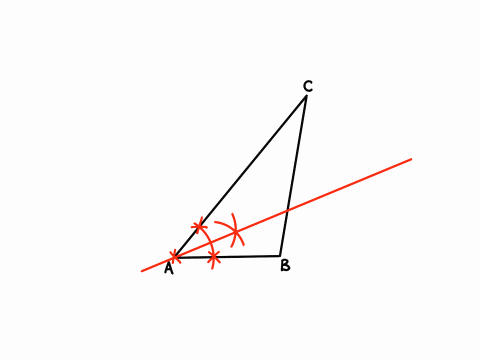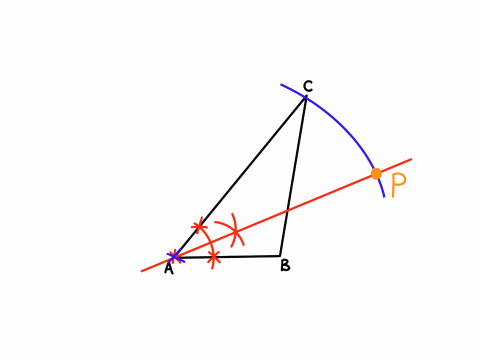
✖️印はコンパスの針を刺す部分
(2)解説「方程式(規則性)」☆☆(3)「関数」☆☆

2番のような問題は、規則性を見つけることを心掛けてください。
この問題だと、6ずつ増えていることが分かりますね。
これにさえ、気づくことができれば簡単に解くことができたと思います。
3番は辺の長さの比が与えられているので、その辺の長さを求めることができれば解けますね。
2番、3番でも大事なことは、まず何をすればいいのかを理解することです。
これはどうやって身につけることができるのか。
その方法は、問題をたくさん解くしかありません。
ぜひ全国の入試問題をどんどん解いてみましょう。
第三問
(1)解説「連立方程式」☆☆

この問題は、問題集に必ず載っています。
ということは、必ず正解したい問題になるってことですね。
この問題からわかることは、普段のワークへの取り組みがいかに重要かということです。
1問1問丁寧にやっていきましょう。
(2)解説「資料の整理」☆☆

(1)(2)は問題集に載っています。
見たことありますよね?笑
ただ、意外とミスが多いのも特徴です。
不等号、階級値で答えることに注意しましょう。
(3)は正直変な問題だなと思いました笑
だって、そうなるじゃんって思ってしまうんですよね。
こういうことを答えさせたいのかもしれませんけどね笑
第四問
(1)解説「合同の証明問題」☆☆☆

※「2組の辺とその間の角がそれぞれ等しいので」の部分で「それぞれ」が抜けていたので訂正させて頂きました。他の部分についても多少変更してあります。
ご指摘して頂いた方ありがとうございました。
ミスがないように精進していきます。
少し難易度の高い証明問題ですね。
でも、少しだけなのでしっかり解けるようにしたい問題です。
まず、証明問題ですることは、上に解説のように長さや角度が等しいところに印を書き込んでいくことです。
当たり前のことですが、結構やらない人が多いのです。
出来なくてもいいので、まず書き込みましょう。
(2)解説「空間図形(面積)」☆☆

(1)は正三角形の面積を求める問題ですね。
これは定番問題です。
これが出来ないと真ん中の学校ですら合格は難しいでしょう。
面積を求める問題で大事なのは、直角を作ることです。
上の解説でも直角を作るために補助線を引いています。
この意識を常に持ってくださいね。
(2)も正直難しくないですができなかった人やできたけど時間がかかってしまった人が多かったのではないでしょうか。
面積を求めるためには直角も必要なんですが 、辺の長さが分かっていないと何も始まりません。
だから、三平方の定理を使ってまず三角形の長さをすべて求めましょう。
そして、次のことに気づけたらすぐ答えが出せますね。
それは、直角三角形であること。
直角三角形は、二辺をそれぞれ二乗したものを足して、残りの辺の二乗と等しくなれば良かったですよね。
これに気づけば、本当に一瞬で終わってしまいます。
第五問
(1)〜(3)解説「グラフを読み取る問題」☆☆

内容的に難しくはないので☆2つにしました。
ただ、文が長い上に、グラフが出てくるとかなり難しく感じる人がたくさんいたと思います。
こういう問題を解けるようになるためには、公式を使えばできるレベルではダメです。
この問題を解けるようには、慣れるしかありません。
似たような入試問題を積極的に解いていきましょう。
(3)はあえて連立方程式で解きました。
理由は、数学が苦手な生徒はこの方が 取り組みやすいからです。
もちろん数学が出来る人は傾きから解ける方がいいと思います。
(4)解説「グラフを読み取る問題」☆☆☆

これは、制限時間がある中で落ち着いてできるかが一番大事だったと思います。
ただ、難しいですね。
この問題は、問題文をしっかり読んでグラフにどんどん書き込むことで答えが見えてくるかと思います。
つまり、公式を使えば解けるというレベルではダメだということですね。
だいぶ増えてきましたが、これからもっと増えていくはずです。
特に上位校を目指す人は、合格できるかの重要な問題になってくるのでしっかり対策が必要になってきると思います。
第六問
(1)解説「規則性」☆(2)〜(3)「規則性」☆☆
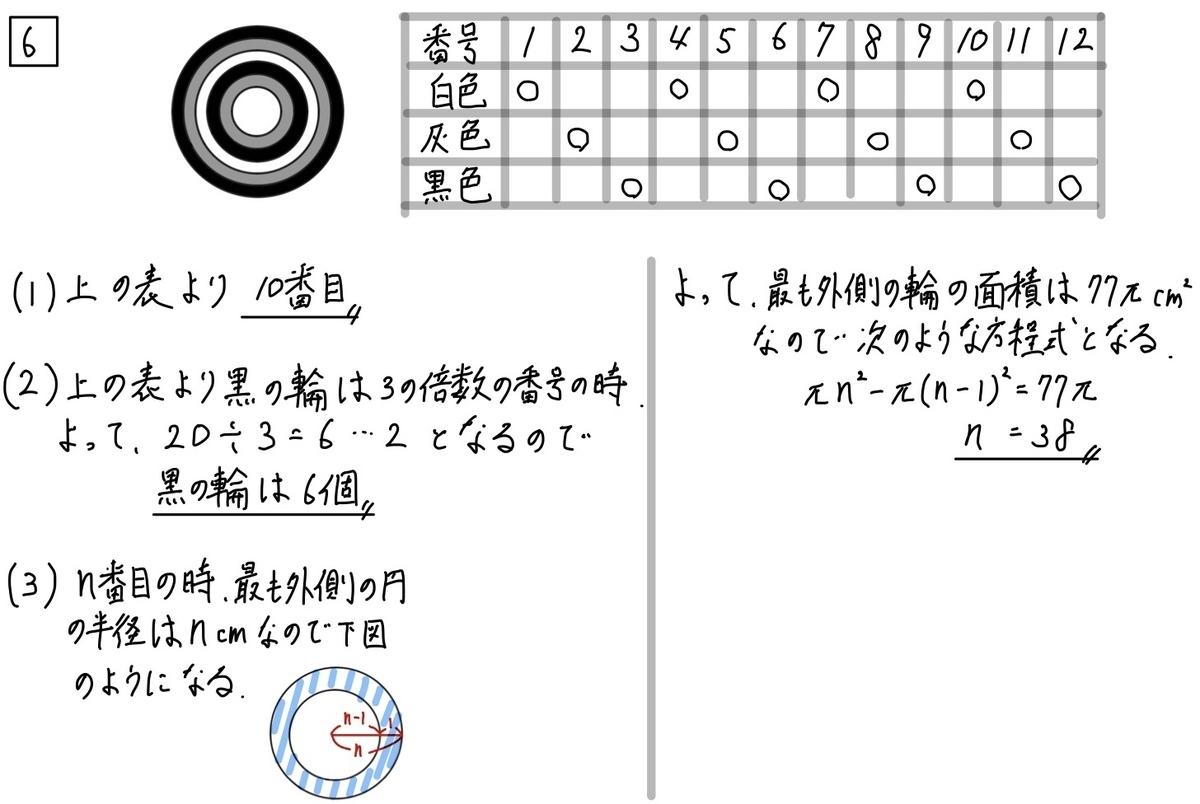
(1)(2)は上のように表を書くことができれば必ず正解できる問題ですね。
とりあえず、規則性がある問題は地道にやれば答えが出ます。
やり方が分からなければこれでokです。
ただ、(2)は上の解説のようにできるようになってほしいですね。
(3)は、上の解説のような簡単な図で構わないので描きましょう。
そして、円の面積を求める必要があるのは明白なので
半径がどうなるか
の一点をしっかり考えましょう。
(4)①解説「規則性」☆☆☆

この問題は、解説のように図を描けるかが勝負です。
しっかり問題文を読んで、状況を理解する力が問われています。
普段からしっかり考える問題を解いてきた人は問題なくできたでしょう。
なぜなら問題の内容自体は難しくないからです。
公式ばかりに頼る勉強は通用しなくなってます。
今まで公式に頼ってきた人は、そういう考えは捨てて考える癖をつけましょう。
(4)②解説「規則性」☆☆☆

これは①が出来ていないと解けない問題ですね。
ただ、解説のように表も組み合わせて考えるとミスなく速く解けると思います。
特に今回a=3という答えにしてしまった人もいるはずです。
確かに、a=3のとき、b=5になるので両方整数になるんです。
しかし、問題文に同じ色であるという条件があるんです。
だから、上のように表にしておくと視覚的に色が違うのが分かりますよね。
参考になればなと思います。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年栃木県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。