
公開日2021/09/11
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
自分の勉強のために解説を書いています。
間違い等あればお気軽に指摘してくれると嬉しいです。
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
第一問
(1)〜(6)解説「計算問題・因数分解・解の公式・球の表面積」☆
(1)97.9% (2)98.1% (3)98.1% (4)86.7% (5)88.8% (6)65.2%

これらの問題は確実に正解したいところです。
いつも正確に計算するためには
普段から丁寧に計算すること
をしっかり心がけるようにしましょう。
・途中式を書かずに、頭で計算しようとする
・あとから見返した時に、どこに計算式が書いてあるかわからない
ような状況の人は特に注意してくださいね。
そして、素因数分解のやり方、解の公式、球の表面積・体積の公式のような覚えなければならないものは確実に覚えましょう。
えーと…と考えているようではダメです。
聞かれたら即答できることを目標に普段から取り組んでくださいね!
(7)解説「角度」☆80.2%

この問題を見た瞬間に何かしたくなりましたか?
もし何もしたいと思わなければ、問題を解く量が足りませんよ!
この問題でしたくなってほしいのは
上の解説のように補助線をひくこと
です!
それができたら、あとは錯角を使って解くだけですね。
数学は意外と覚えていれば解ける問題が多いです。
覚えていれば解けた問題に出会うたびに、しっかり覚えていきましょう。
これを入試までに繰り返していけば、必ず結果に結びつきます。
そのためにも毎日勉強し続けましょう!
(8)解説「中央値・相対度数」☆☆65.9%

中央値の求め方をしっかり分かっていない人が毎年います。
もし、自分も分かっていない!って状況なら上の解説をしっかり見ておいてください。
特に注意してほしいのが、奇数と偶数で微妙に変わるところですね。
そして、相対度数って難しそうな言葉が出た途端、
思考停止状態になってませんか?笑
でも、これって小学生で習った割合と全く同じなんですよね。
だから、相対度数は割合のことだと読み直してもう一度解いてみてください。
そうすれば、きっと解ける人が増えるはずです。
これでも解けない人は、小学生で習った割合が苦手なまま今まで過ごしてきたのでしょう。
今がやり直しができる最後のチャンスだと思って、小学5年生の教科書を開いて勉強し直してみてください。
もう教科書がないって人は、本屋に走って、割合の解説が書いてある本を探して立ち読みして理解しちゃいましょう。
それでもダメな人は、学校、塾の先生に急いで聞いて解決しちゃいましょう!
第二問
(1)解説「速さ」☆☆86.8%(2)「連立方程式の利用」☆☆
(2)ア88.8% イ85.7% ウ85.1%
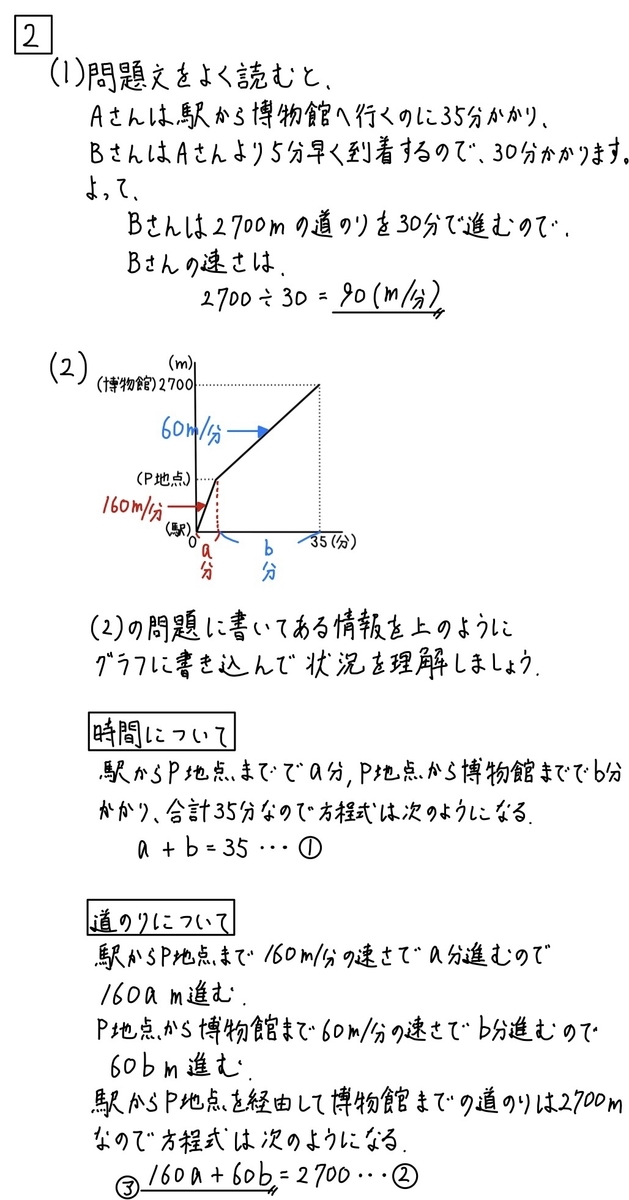

このような問題を見ると、そっと問題集を閉じたくなる人いませんか?笑
でも、学校や塾の問題集に必ずと言っていいほど載っている問題ですよね。
初めはゆっくり時間をかけて解いても構いません。
それでも、解けないって時は学校、塾の先生に聞いてみましょう。
(もちろん、解説は読んでくださいね。)
その時に次のように質問してみてください。
「先生なら何に注目して解きますか」と。
僕ならBさんのグラフが書かれていないことに注目してごらんって答えると思います。
なぜBさんのグラフが書かれていないのか。
それはBさんのグラフが書いてあるとすぐに分かってしまうから。
つまり、Bさんのグラフを自分で書くことを求められている問題であると僕は思います。
(1)、(2)の問題が解けなかった人は、上の解説をしっかり読んでくださいね。
(3)解説「連立方程式の利用」☆☆39.4%

この問題は、(1)の問題の時点でBさんのグラフを書いていればすぐに解き方を思いついた人も多かったのではないでしょうか。
また、真ん中くらいの高校を目指す人はこのような問題を正解できれば合格にグッと近づきますね!
追いついたり、出会ったりする問題は、
直線のグラフの交点が答えになる
ことが多いです。
つまり、問題文で「BさんがAさんに追いつくのは…」を読んだ時点で、
直線の式を2つ求めて、
その式を連立方程式で解くんだな
という流れが頭の中に浮かぶようになっていればバッチリですね。
今回ダメだった人は次で思いつくようにしていきましょう!
第三問
(1)解説「相似の証明」☆☆ⅰ89.0% ⅱ91.2%

証明問題は苦手な人は意外と多いです。
もちろん、難しい問題が出題されることもありますが、
問題のパターンはそこまで多くありません。
なぜなら、合同・相似・二等辺三角形・平行四辺形になる条件は限られているからです。
自分で文章を書かなければならないので難しいと感じるかもしれませんが、証明問題を1週間くらい解き続けてみてください。
「あ、また同じ問題が出てきた」ってだんだんなってきて
苦手から得意な問題にきっと変わってくるはずです!
騙されたと思って、苦手な人はやってみてください!
入試に出てくる証明問題を解きたい人は下の問題集がおすすめなのでぜひ解いてみてください!
(2)解説「円と相似(辺の長さ)」☆☆42.3%

相似の図形を頭の中でイメージするのって意外に難しかったりしますよね。
僕もどちらかと言うと苦手な方です。
だから、僕の場合、解説のように大きさを微妙に変えて相似な図形を2つ書いちゃいますね。
もちろん、アルファベットもしっかり書きます。←これがとても大事なんです。
これをしておけば、間違った比例式を作ることがなくなります。
男子に多いことなんですが、
頭の中でやろうとして、全く図を描こうとしない子が毎年必ずいます。
天才的に図形が得意であればいいのですが、
間違えていることの方が圧倒的に多いんですよね。
図を描くことがめんどくさいのかもしれませんが、
結果的に図を描いた方が正確に答えに辿り着くことが多いです。
しかも、図を描いた方が速いことが多いですね。
その問題にそんなに時間かけてどうするの…って言う生徒が毎年います。
これを読んだあなたは大丈夫ですか?
もしドキってしたなら、今からでも考え方を改めてみてください!
最後にこの問題の解く流れだけ簡単に書いておきますね。
辺の長さを求める問題ですが、
ポイントになるのが1つ前の問題です。
なぜ最初に相似の証明問題が出題されたのかを考えてみてください。
その理由は、
この後の問題で相似を使って問題を解く
からです。
これは必ずではないですが、
僕の感覚では8〜9割はこの考えが通用します。
頭の片隅にでも置いておいてもらえると嬉しいです。
(3)解説「円と相似(三角形の面積)」☆☆☆32.5%


この問題のポイントは
三角形BCEが正三角形であること
に気づくことですね。
まあ、見た目からして正三角形なので
分からなければ、正三角形として問題を無理やり解いていってもいいと思います。
ただ、試験の時に限ってですけどね。
正三角形になる理由は上の解説に書いてあるので
しっかり読んでみてくださいね。
正三角形だと分かれば、辺の長さが与えられているので
面積を求められますね。
正三角形の辺が分かっていて、面積が求められない人は
上の解説をしっかり読んでおいてくださいね。
2等辺三角形でも同様のことが言えますが、
頂点から底辺に向かって垂線を下ろす
ってことを当たり前のようにできるようにしておきましょう。
ここで注意してほしいのが、
正三角形の面積の求め方を公式のように覚えている人です。
もちろん、公式を覚えるのも大事ですが
その公式の導き方を分からずに使っているのであれば
今後、数学で確実に苦労します。
使うことを否定はしませんが、もし使うのであれば公式の導き方まで理解してくださいね。
(4)解説「空間図形(体積)」☆☆☆☆1.0%



この問題は難しいですね。
トップ校を受験する人は、初見で解けなくてもいいので
解説を読んでしっかり流れを理解してほしいです。
その他の人は、解けなくても全く問題ありません。
この問題を解く最初の流れは、次のような感じです。
体積を求めるためには、
・底面積
・高さ
が必要。
↓
・底面積の一部(三角形BCE)は面積が分かっているから、残り(三角形ABC)はどうやって求めよう。
・高さは球の半径と同じだから、他の場所で球の半径となる場所を探せばよさそう。
この流れがまず頭に思い浮かばないと、何をしたらいいのか分からない状態になるかと思います。
ここが分かれば、上の解説のように解いていく流れが理解できるかと思います。
第四問
(1)〜(2)解説「二乗に比例する関数・反比例(座標・比例定数)」☆☆
(1)81.7% (2)83.3%

この問題はどの学校を受験する人にもできるようになってほしい問題ですね。
内容的にそこまで難しくありませんので、
もしできなかったって人がいれば、諦めずにできるまでチャレンジしましょう!
上の解説を読んでも分からなければ、学校、塾の先生に聞いてくださいね!
(3)①解説「二乗に比例する関数(座標・変域)」☆☆☆
ア54.8% イウ40.8%


この問題(①)で出てくる点Eは次の問題(②)で出てくる点Eとは異なるので注意してください。
この問題は、(1)を間違えると全滅します。
計算ミスには気をつけてくださいね!
ただ、考え方が少し難しいですね。
三角形OACと三角形OBDの面積比が3:1であることをうまく利用して解かなければなりません
ここをうまく利用して
三角形OAE:三角形OEC:三角形OBDの比を出せれば
(ア)の答えにたどり着くかと思います。
ここができれば、(イ)(ウ)はサービス問題ですね。
定期試験にもよく出題される問題なのでしっかり正解したいところです。
ただ、答えが2≦y≦8になった人は要注意です。
何を間違ったのかを図をしっかり書いて確かめてくださいね。
(3)②解説「二乗に比例する関数(座標)」☆☆☆6.8%


この問題は難しく感じるかもしれませんが
よくある問題なので何をすればいいのかはわかってほしいです。
この問題で注目してほしい言葉は
「3辺の長さの和が最小となる」
です。
(よく問題集に載っている表現は「AP+BPの辺の長さが最小となるのは〜」ですね。)
これがあると、必ずと言っていいほど
線対称
を利用して解きます。
塾のワークにも必ず1問くらいあるはずです。
覚えてないなーって人は中2のワークを探してみてください。
確認はしてないですが、学校の問題集にもあると思います。
この線対称の考え方が思いつけば、
きっと答えに辿り着くはずです。
偏差値60前後以上の学校を目指す人は確実にできるようになってほしい問題ですね。
第五問
(1)解説「場合の数」☆☆37.9%


上の解説では、樹形図と計算で求める2つの解説を載せてみました。
これくらいの量であれば、全部書き出してもそこまで時間がかからないので
全部書き出して解くのも僕はありだと思います。
ただ、計算の方法は学校では習わないと思うので無理にやる必要はありません。
余裕がある人のみ、知っておきましょう。
(2)解説「場合の数」☆☆37.6%

(1)で樹形図を完成させた人は、数えるだけでしたね笑
地道にやればできる問題は、確実に正解するようにしましょう!
(3)①解説「場合の数」☆☆11.8%

このような問題は樹形図で説いてもいいですが、
できれば上のように場合分けをして
考えること
を意識して解いてほしいですね。
そうじゃないと、このような問題を解く意味が半減してしまう気がします。
もちろん、入試の時は正解することが最優先なので
樹形図で解くことも大事だと思います。
しかし、何も考えずに解いていると、
ある一定のレベルから上に行くことは難しくなってきます。
そうなりたくない人は、ぜひ考える癖をつけてくださいね!
(3)②解説「確率」☆☆2.9%

この問題を解いていると、時間が厳しくなると思うので後回しにする方が賢いと思います。
満点を目指すのではなくて、取れる問題を取ることが入試では非常に大事ですからね。
この問題は上の解説をしっかり読んでほしいところですが、
少しだけ意識してほしいことを書いておきます。
それは
ルートは2乗の積なら整数になること
です。
(これをわかっていない人が意外に多いです。2乗だけなら分かっているのだけれども)
ここが分かっていると、この問題で
6が入れば整数にならないことがすぐにわかるはずです。
なぜなら、素因数分解すると全体で3の数が3つしかないので
2乗を1つ作ると、3が1つ余ってしまうんですよね。
だから、上の解説では1回も6が含まれていないんですよね。
6が入ると整数にできないので。
ここに気付かなかったら、かなり時間がかかったはずです。
第六問
(1)解説「星形正n角形(手を動かして考える問題)」☆67.3%

この問題は手を動かせば解ける問題です。
確実に正解したいところですね。
いまいち分からないって人は、下のアニメーションを参考にしてから自分で実際に書いてみてくださいね!
(1)解説「星形正n角形(手を動かして考える問題)」アニメーション
ア円周を10当分する点を取る

イ円周を11当分する点を取る

ウ円周を12当分する点を取る

(2)解説「星形正n角形(角度)」☆☆☆①16.9%②13.1%

この問題は意外と意外と難しかったのではないでしょうか。
問題文に書いてある
「おうぎ形の弧の長さは中心角の大きさに比例する」
から
「■:7=2x:360」の■にどんな値が入るのか
を読み取るのは難しいです。
ただ、説明を聞けば「それだけ?」ってなる内容です笑
ここで意識してほしいのは
左と右の比が対応している
ってことです。
■:7=2x:360では
■と2xが
7と360が
それぞれ対応しています。
ここに気がつくと(中1の内容なので、できれば知っていてほしい)
すんなり答えに辿り着くはずです。
(3)解説「星形正n角形(角度)」☆☆☆4.8%

この問題は上のように具体的に考えて、
どんな規則があるのか
を見抜く必要がありました。
気付かないと解けない問題になるので、
他の問題を優先する、または、見直しに時間を使うのもありな気はします。
(4)解説「星形正n角形(角度)」☆☆☆9.8%



この問題は間違いなく捨てるべき問題ですね。
これを解いていたら、間違いなく時間が足りません笑
ただ、非常に面白い問題です。
僕も解きながら、こんな図になるんだ〜!
って解いていて楽しめました笑
こういう問題を作れる人は本当に尊敬します笑
この問題にチャレンジしようと思う人は、
ぜひ、時間を気にせずに
手を動かして
解いてみてください!
総括
全体通して解いてみた感想は、
考える問題が多い
の一言ですね。
公式を使えば簡単にできる問題ばかりを解いている人はかなり苦戦したでしょう。
めちゃくちゃ難しい問題は多くないですが、
普段から考える習慣がない人はかなり点数が低いはずです。
高得点を目指したい人は、
まず、公式を使えば得点できる問題は当たり前のように解けるようにしましょう。
その上で、入試問題のような難易度の高い問題を2、3日1問でもいいので解くようにするといいでしょう。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
上位校を目指す人へおすすめの問題集
2021年に行われた全国の入試問題が収録された問題集です。
特に上位校を目指す人は必ず解いている!
と言っていいものになります。
意欲がある人はぜひ購入しどんどんチャレンジしましょう!
今回は2021年兵庫県公立高校入試数学問題をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。