
公開日2020/10/04
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
また、大阪の公立高校入試倍率、部活動、大学合格実績、他の公立数学解説についてもっと知りたい方は
こちらをクリック!
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題はこちら
引用元:長野県教育委員会
大一問
(1)〜(4)解説「計算問題」☆

基本的な計算問題ですね。
(5)解説「奇数」☆(6)「因数分解」☆☆

(5)は見た瞬間分かるようになっておいてほしいです。
奇数は2n+1,2n+3
偶数は2n,2n+2
のようになることは最低覚えておきましょう。
(6)の問題は、結構軽視する人が多い問題ですね。
「え、こんなことしなくても普通に計算したらいいやん」
って声が聞こえてきそうです笑
僕もそう思います。
でも、いろんな引き出しは持っておくべきです。
1つのやり方しかしないって頑固じじいかって言われちゃいますよ笑
(7)解説「反比例」☆(8)「変域」☆☆
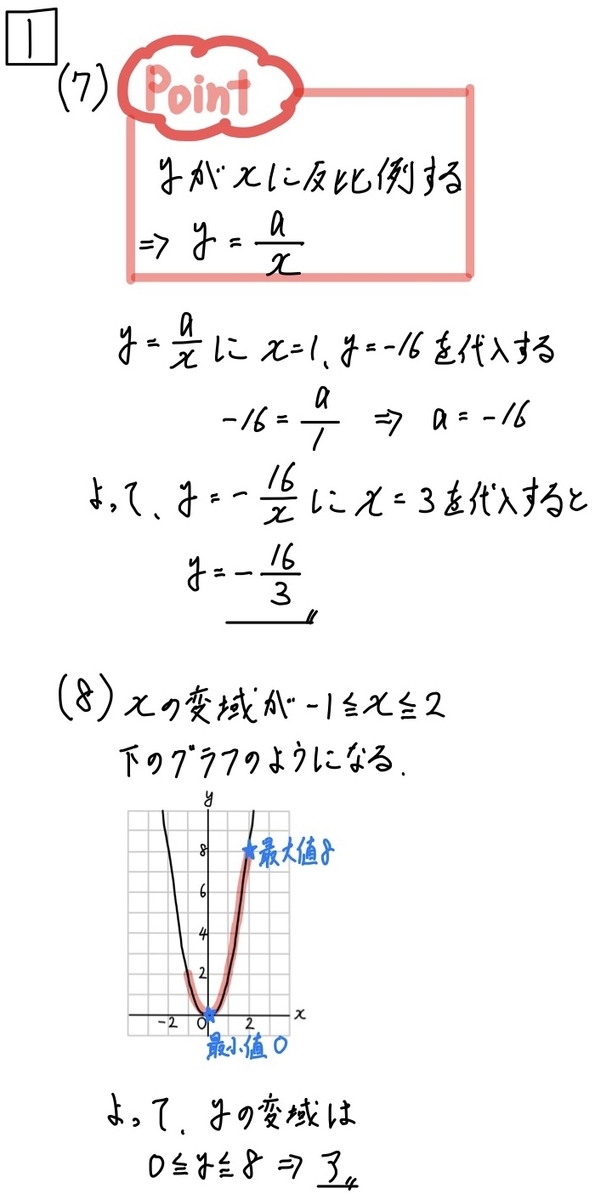
(7)は反比例の問題です。
反比例の式を書けって言われたら、すぐに書けるようにしておきましょう。
そして、解説に書いている公式だけでなく
a=xy
の式も覚えているとよりいいですね!
(8)はミスがとても多い問題です。
そして、ミスする人のほとんどは自分勝手のやり方ばかりする人です。
素直に勉強することはとても大事です。
この問題は、必ずグラフを描いて解くようにしましょう。
もちろん、慣れてくれば描かなくても構いません。
しかし、なぜかそこまでできないのに頭の中でしようとする人がかなりいます。
そして、必ずと言っていいほど間違えるのです笑
もう一度言いますね。
グラフを描いて考えましょう!
(9)解説「確率」☆
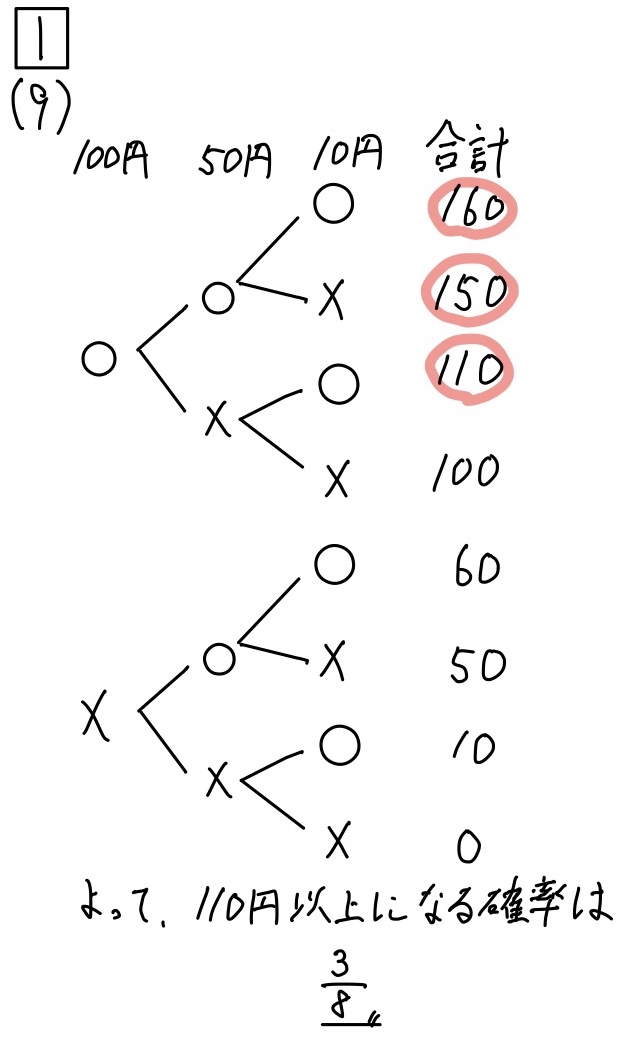
これはかなり基本的な問題ですね。
中学受験に出てきそうな問題です。
これは確実に正解したい問題になります。
(10)解説「コンパスの作図」☆

これは線対称と作図を絡ませた問題ですね。
しかし、ほとんど基本的な問題に変わりはありません。
確実に正解してほしい問題です。
ちょっと描き方分からない人は下の解説アニメーションを参考にしてください。
(10)解説アニメーション「コンパスの作図」

✖️印はコンパスの針を刺すところ
(11)解説①「角度」☆②「平行四辺形の性質」☆☆

①は中点連結定理などが分からなくても
何となくで正解する人が多いかもしれませんね。
こういう問題こそ、しっかり解説を読んで理解するようにしてほしい問題です
正解したから解説読まなくてもいいやはかなりもったいないですね。
②は平行四辺形になる5つの条件を覚えているかどうかの問題ですね。
「???」
って頭の中がなってませんか?笑
そういう人は、今すぐに中2の教科書を開いて覚えてください。
かなり大事なことです。
こういう問題だけでなく、平行四辺形の証明問題でも必要になってきます。
ってことは、覚えていないと解けないということですからね。
第二問
(1)解説「資料の整理」☆

この問題は正直難しくはない。
ここで大事になってくるのは、
階級、階級値、相対度数、中央値、最頻値などの言葉が出てきたときに何を答えるのかがわかっているかどうか
だけ。
つまり、勉強が得意・苦手とかは関係ない。
勉強をやっているか、やっていないかだけ。
だから、塾に行っているのにこの部分ができない場合かなりヤバいかも?笑
上の③の解答しなければならない理由は書きませんでした。
②、③をまとめたものが理由になるので
これくらいは自分で考えて言葉にしてみましょう。
(2)解説①「三平方の定理」☆☆②「体積」☆☆

ここはしっかり正解してほしい問題になります。
偏差値45以上の学校を受験予定の場合、この問題ができないと厳しいイメージがあります。
(これは僕の肌感覚です笑)
この問題ができない場合、
そもそも三平方の定理や円の面積を求める公式を覚えていない可能性が非常に高いです。
まず、この部分をしっかり押さえましょう。
(3)解説①「平行四辺形の公式」☆☆②「平行四辺形の公式(方程式)」☆☆☆
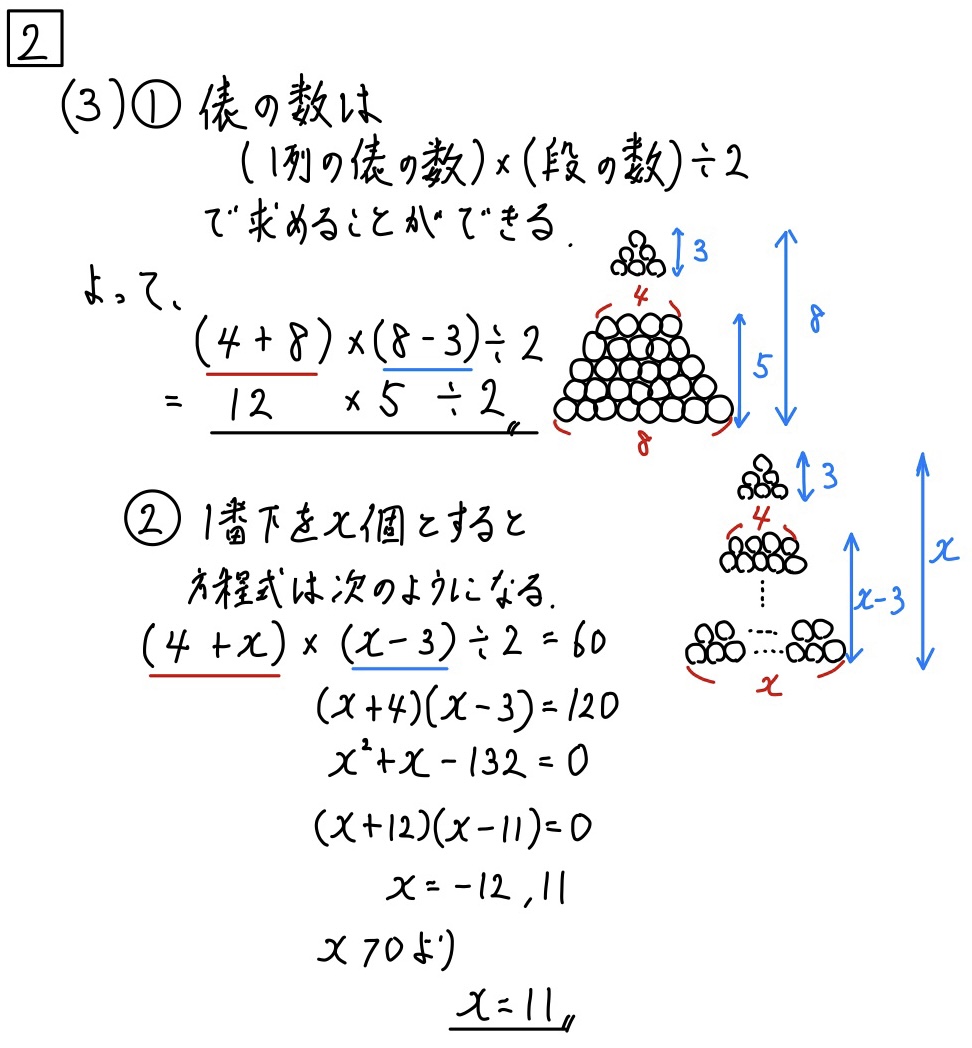
これは、平行四辺形の公式の作り方の問題ですね。
この部分に気付くとかなり解きやすくなりましたね。
また、上の解説に図を書いていますが、このように書いて考えると非常に分かりやすくなりますね。
参考になればなと思います。
第三問Ⅰ
Ⅰ(1)解説「一次関数の利用」☆

これは見た瞬間に解けるようになってほしいです。
なぜなら
代金が等しくなるのは、2つのグラフが重なったところ
だからです。
Ⅰ(2)解説「一次関数の利用」☆(3)〜(4)「一次関数の利用」☆☆

この辺りの問題をしっかり解けるようにするためには
慣れ
が必要です。
この問題は中2の2学期で習う内容になります。
だから、この時にしっかり考えて解くようにするくせをつけておく
ことが受験時にできるように生きてきます。
しかし、苦手な人はどうやって解いていくか全く分からないはずです。
だから、そういう人は先生にこう質問してみてください。
「先生ならどんなふうに解きますか?一度、先生が解いているところを見てみたいです。」
これを一度でも見ていると、問題を解くときに見るべきポイントを掴みやすくなるはずです。
第三問Ⅱ
(1)解説「一次関数の利用(考える問題)」☆☆☆ (2)「一次関数の利用(読み取る問題)」☆☆☆

第四問Ⅰ
Ⅰ(1)解説「証明問題(穴埋め)」☆☆

穴埋めの問題にしては少し難しめですね。
でも、空欄の前後だけである程度答えは出ると思います。
ただ、この問題は記述の証明問題で出たとしても解けるようにしておきましょう。
この問題は結構出題されるタイプの問題なので。
Ⅰ(2)解説「証明問題(記述)」☆☆ (3)「2組の辺の比」☆☆

(2)の証明問題は定番って感じですね。
個人的には、(1)の穴埋めの証明問題を記述にしてほしかったですね。
とりあえず、ここで押さえてほしいことは
同じ弧から出る円周角は等しいということ
です。
まあ、これは分かっている人が多いです。
しかし、それは角度の話の時だけ。
証明問題になると、できなくなっていることが多いです。
これは、証明問題を解く量が単に少ないだけです。
(もしくは、答えを写して考えていないか笑)
↑このパターンは実はかなり多い笑
(3)はできましたか?
これは証明問題でも使う内容です。
「2組の辺の比とその間の角がそれぞれ等しい」
という相似条件で使います。
ただ、問題集にあまり載っていないんですよね。
だから、解き方が意外と知らない子が多くて困ります。
だから、この問題も出来はそこまで高くないと思います。
第四問Ⅱ
Ⅱ(1)解説「角度」☆☆

この問題は、問題文中の情報をしっかり図に書き込んだかどうかが全てだと思います。
なぜなら、この問題は正三角形の存在に気付かなければなりません。
しかし、正三角形という言葉は本文に書いていません。
図形の問題は、必ず与えられた情報をどんどん図に書き込んでいきましょう。
これが図形をできるようにしていく一番の近道です。
Ⅱ(2)解説「平面図形(半径)」☆☆☆
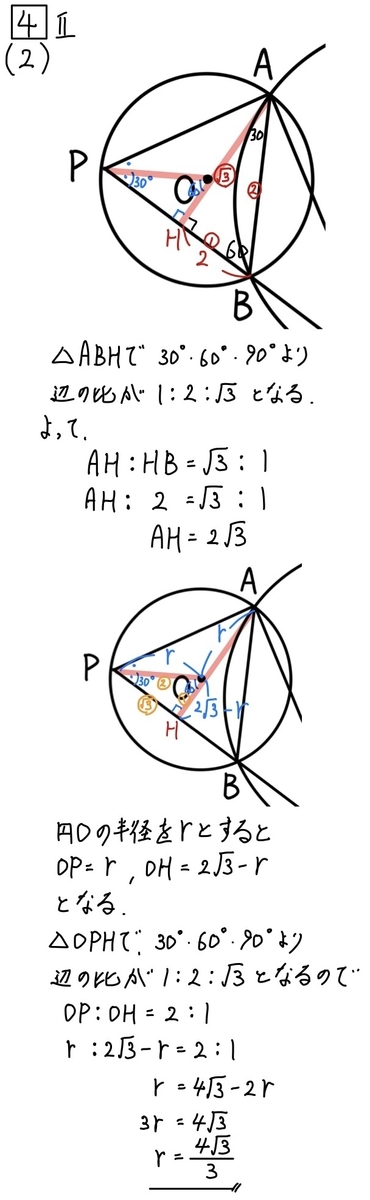
この問題を解く上で大事なことは、
「補助線を引かなければならないことに気づく」
かどうかです
今回は、半径を求めなさいということなので
中心を通る線が必ず必要です。
しかし、最初の図の状態では書かれていません。
だから、上の解説の赤のマーカーのような補助線を引かなくてはいけませんでした。
この時に意識してほしいのが正三角形があるので、
補助線を引くことで30・60・90の直角三角形が作れるということ。
ここまでのことができれば、答えに辿り着いたようなものです。
あとは、上の解説を見ていただければ解き方の流れはわかると思います。
Ⅱ(3)解説「平面図形(最大面積)」☆☆☆☆

この問題は何が難しいかって
「面積が一番大きくなるのはどこなのかわかる」
ことですね。
ただ、次のことを意識してみるとそこまで難しく感じなくなると思います。
面積が大きくなるということは、辺の長さも大きくなるということですよね。
ということは、
円の中で作れる最大の直線の長さはどこなのか
に気付ければ正解に近づきます。
この答えを書くと、
それは円の半径ですよね。
円の中で作れる直線で一番長いのは円の半径なのですから。
ここで一度上の解説の図に戻って見てください。
納得できましたよね?
あとは、上の解説の流れで解いてみてください。
きっとできるはずです。
必要ないかもしれませんが、三角形の動きをアニメーションで表現してみました。
気になる人は見てみてください。
Ⅱ(3)解説アニメーション「平面図形(最大面積)」

どうでしょうか?
かなり分かりにくと思いますが、
一応、半径を通った時に面積が一番大きくなっているはずです。
参考になれば嬉しいです。
Ⅱ(4)解説「平面図形(面積比)」☆☆☆

初めの方で相似の証明問題がありましたよね?
あれをここでも意識していればすぐに解き方が思い浮かんだ人も多いかと思います。
そして、相似の三角形を見れば、面積比で解けるようにしておきましょう。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
今回は2020年長野県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。