
公開日2020/07/16 更新日2020/11/29
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題を見たい方はこちらからどうぞ。
引用元:Web東奥
第一問
(1)解説「計算問題」☆

ここは基本的な問題ばかりです。
ただ、1つだけ
解きにくくしているのがありました。
それは、エの問題です。
前から順番に展開すれば、問題ありません。
しかし、因数分解をしようとすると、
ミスする人が出てくるはずです。
なぜなら覚えている公式と順番が入れ替わっているから。
だから、上の解説のように前後入れ替えてあげると解きやすくなりますね。
(2)解説「方程式」☆(3)「素因数分解」☆(4)「連立方程式」

(2)は文章通りに式が作れるかですね。
数学が苦手な人の多くは、
これができません。
このタイプの問題は、
小学生で習います。
おそらく、小学生の問題でもできないと思いますので、
小5、6年の似たような問題を解くことをお勧めします。
(3)の素因数分解は特に問題ないと思います。
ただ、ここで注意してほしいのが
素因数分解したときの並び順です。
なるべく、数字が小さい順に書きましょう。
模範解答は小さい順で必ず書いています。
だから、並び順が違うと間違って採点される可能性が出てきます。
ぜひこういうところまで考えられるようになるといいですね。
(4)は代入法で解くようにしましょう。
もちろん、加減法で解くことはできます。
しかし、この式を見て加減方で解こうとするのはナンセンスです。
しかし、数学が超苦手で加減方でしか解けないって人は構いません。
定期試験で20点台以下をとるよう人ですね。
(4)解説「反比例」☆☆(6)「標本調査」

(5)は反比例の知識がしっかり分かっていれば
問題なく解ける問題です。
これを間違った人は、
反比例のグラフをしっかり書いて1つ1つ丁寧に確認してください。
(6)のような問題は苦手な人が多いです。
このタイプの問題が苦手なら、
これからの入試問題は苦労するでしょう。
ただでさえ、文章がどんどん長くなってきてますからね。
できれば、早いうちに文章の長い問題は解くようにしておきましょう。
いろんな都道府県の入試問題を見てみてください。
普段解いているワークだと、そこまで長い問題を解くことはほとんどありません。
ぜひ次の問題集を購入してみてくださいね。
特に上位を目指している人にはおすすめです。
↓↓↓↓↓↓↓↓↓
(7)解説「角度」☆☆(8)「球の表面積」

(7)は補助線が引けるかどうかがすべてです。
なぜ補助線が引けるのか。
いろいろ考え方があると思いますが、
『くの字』『逆くの字』があるときに
補助線を引くように僕は教えています。
ここができれ、同位角、錯覚、二等辺三角形を使って求めることができますね。
(8)の問題は注意することが2つあります。
1つ目は、黄色の切り口の面積を求めることを忘れないこと。
意外と忘れる人が多いです。
2つ目は、『π』のつけ忘れ。
これはめちゃくちゃ多いので要注意です。
第二問
(1)解説「方程式」☆

この問題は、地道にできるかどうかですね。
これが分からないという場合、
算数から指導し直す必要があるか
それとも
やる気がないか
のどっちかですね。
最後の問題はできないかもしれませんが
しっかり調べれば全く解けないことはないはずです。
勉強が苦手であっても、こういう問題を粘り強く解いてくれる生徒に入学してほしいと学校側は思うんじゃないでしょうか。
(2)解説「円周角・確率」☆

円周角の定理について分かってなければ解くことは難しいかもしれません。
しかし、円周角の定理はある程度のレベルまではほとんどの人ができるようになります。
この意味では、入試の範囲外になったのは残念でなりません。
だから、この問題もしっかり手を動かしせば、答えにたどり着くことができるはずです。
もちろん、工夫しながら解くことができれば一番いいですが、
別にできなくても構いません。
まず、しっかり手を動かして答えに辿り着けるようにしましょう。
そして、その後、もっと良いやり方が知りたければ
そのときに学べば良いです。
第三問
(1)解説「三平方の定理・円錐の体積・角度」☆

これらの問題は、問題を見たら解き方が思い浮かぶようにしましょう。
全部基本的な内容なので、すぐに思い浮かぶようなレベルにしておくべきです。
特に、
(1)ウはしっかりできるようにしましょう。
結構できない人が多いです。
しかし、同じような問題を何回も繰り返せば絶対にできるようになります。
(2)ア解説「相似の証明問題」☆☆

証明問題ですが、穴埋め問題なので解きやすいですね。
ただ、この問題は
穴埋めではなく、最初から最後まで証明をしてほしいです。
途中の辺の比でつまづく人が結構いると思います。
(2)イ解説「平面図形(面積比)」

面積が何倍かを求める問題は、
対象になっている部分の面積比を求める必要があります。
このときに大事になってくるのが、
相似の三角形、等高三角形(高さが等しい三角形)に注目して面積比を求めていくことです。
これは繰り返しといて慣れるしかないと思います。
すぐにはできないと思うので、徐々にできるようにしていきましょう。
何事においても繰り返すことがとても大事です。
第四問
(1)解説「二乗に比例する関数(変域)」☆☆(2)「直線の式」☆☆

この2問は基本的な問題になります
つまり、間違うと周りと差がついてしまう問題です。
だから、確実に正解できるようにしておきましょう。
できれば、2〜3分ほどで必ず終わっているレベルが望ましいですね。
もちろん、2問合わせての時間ですよ!
(3)解説「二乗に比例する関数(式・座標)」☆☆

この問題も基本的な問題になります。
イは一見難しそうに見える人もいるかもしれませんが、
その人は、明らかに勉強不足です。
このレベルが解けるようにならないと、
偏差値50以上の学校はかなり厳しいと思います。
そういった学校を目指している人は確実にできるようにしておきましょう。
第五問
(1)解説「図形とグラフから読み取る問題」☆

この問題は中学入試でよく見ました。
だから、すこーし高校入試で出るのは違和感があります笑
で、この問題ですが
上の解説画像の図とグラフをしっかり対応させて見ましょう。
特に、この問題ができなかった人は目を大きく見開いて見てください笑
水がここまで入れば、グラフはここまでくるなっていうのがわかることが大事です。
(2)解説「図形とグラフから読み取る問題」☆☆

(2)の問題を解くためには以下のことがわかる必要がある。
- 1分あたり高さがどれだけ上がるか
- 底面積が同じなら、場所が違っても1分あたりに上がる高さは同じであること
- 底面積が2倍になったとき、1分あたりの上がる高さは半分になること
この3つをしっかり押さえることができていれば、すぐに解けると思います。
もし1度目で解くことができなければ、
この3つのヒントを頭に入れてもう一度チャレンジしてみるといいですね。
(3)解説「図形とグラフから読み取る問題」☆☆
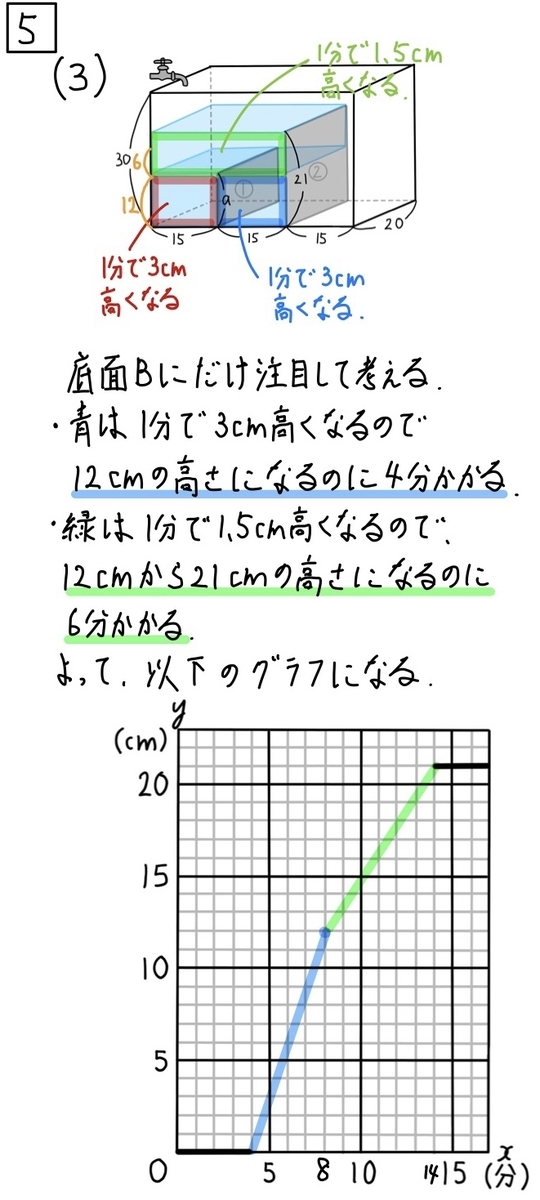
この問題は底面Bの高さに関するグラフを書く問題であること忘れないように。
上の解説のように
- 青のところで1分あたりにどれだけ高さが上がるか
- 緑のところで1分あたりにどれだけ高さが上がるか
この2点をしっかり見ることができれば割と簡単に解くことができます。
(4)解説「図形とグラフから読み取る問題」☆☆

20分後の底面Cの高さを考えなければならない。
ただ、ここでまず考えなければならないのは
14分後の水の状態である。
その図を上の解説に書いています。
ここがわかると、底面Cに水が入っていく時間は6分間ということになる。
つまり、底面Cでは1分で3cmずつ高さが上がっていくので
6分後は18cmとなる。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年青森県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。