公開日2020/07/06
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題を見たい方はこちらからどうぞ。
引用元:紀伊民放
第一問
問1(1)〜(5)解説「計算問題」☆

これらの問題について、
特にいうことはありません。
計算ミス、符号のミスなどに
気を付けてしっかり正解にしましょう
問2解説「因数分解」☆問3「平方根」☆

問2は因数分解するだけですね。
因数分解の公式は全て覚えましたか?
少しでもドキってした人は
復習してください。
ここは余裕になっていないと絶対にダメなところです。
問3も難しくないですね。
√1=1
√4=2
√9=3
√16=4
・
・
・
スラスラ言えるようにしておきましょう。
これさえ言えていたら、すぐに答えが出せますよ。
そして、できれば
11の二乗
12の二乗
13の二乗
14の二乗
15の二乗
などもスラスラ言えるようになっていると、
個人的には19くらいまでは言えるようになってほしいですね
問題を解くスピードが上がります。
ぜひ余裕がある人は覚えておいてくださいね
問4解説「角度」☆☆問5「確率」☆☆

問4は折り返しの問題ですね。
当たり前なことなんですが、
折り返した部分の角度が同じになることを
しっかり押さえておいてくださいね。
ここを見逃していると、
絶対に解くことができないので。
問5は一見めんどくさそうな問題ですよね。
ただ、上のように工夫してあげると
解きやすくなります。
結局、花子さんの数字の方が大きくなる時を
探せばいいだけになるんですよね。
ぜひ参考にしていただければなと思います。
第二問
問1解説「円錐の体積」☆☆問2「傾きの範囲」☆☆
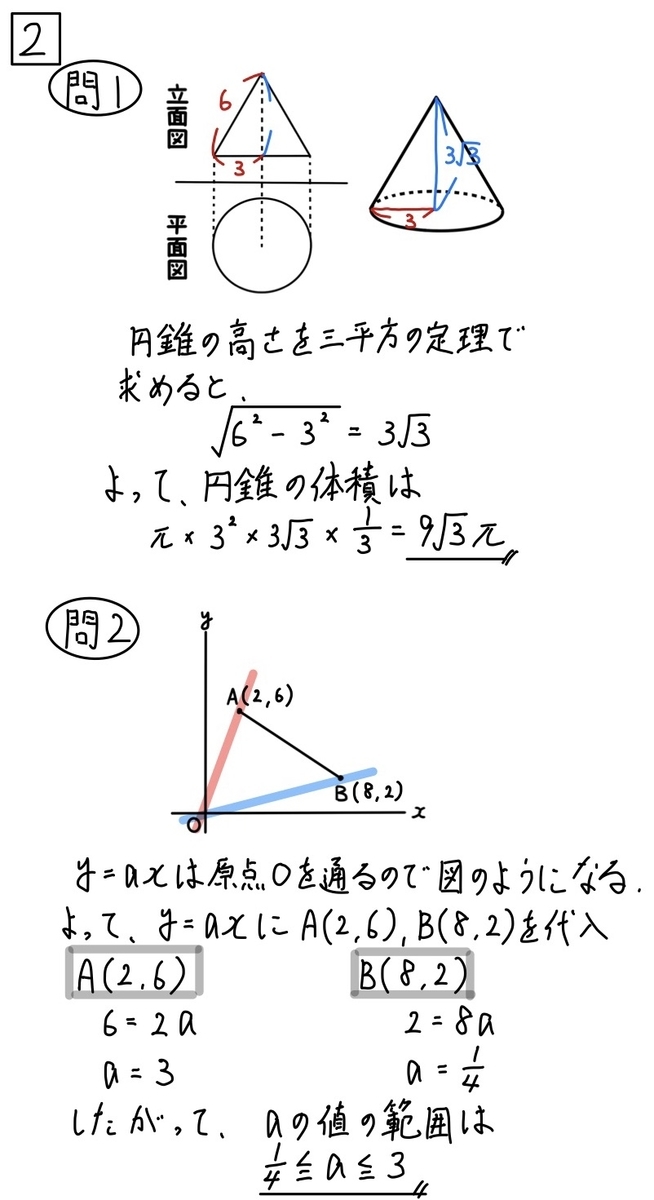
問1に関して
立面図と平面図の違いはしっかり分かっていますか?
図を見れば、何となくわかる人もいると思いますが、
しっかり言葉の意味も知っておきましょう。
立面図は、正面から見たときの図
平面図は、上から見たときの図
というだけです。
簡単ですよね。
この問題は、円錐の体積を求める問題です。
円錐の体積を求めるのに必要なことは
円の半径、円錐の高さ
ですね。
今回は、高さを求める必要がありました。
これは、三平方の定理を使えば簡単に求めることができます。
そして、先が尖っている体積を求めるときは、
1/3をかける必要があります。
忘れないでくださいね。
そして、もう1つ忘れちゃダメなものがありますよね?笑
気づいていない人は危ないかもです。
それは、
π
です。
非常につけ忘れる人が多いので
絶対に忘れないでください!
問2は、傾きの範囲を求める問題ですね。
これは、必ず問題集に載っています。
必ずできるようにしましょう。
これの解き方が思いつかない人は、
勉強量が少ないと言わざるをえないです。
もし、思いつかなかった人は、
これからしっかりやればいいだけです。
最後まで諦めずにやっていきましょうね!
問3解説「資料の整理」☆☆問2「連立方程式の文章題」☆☆

問3(1)は、
階級の幅
最頻値
中央値
相対度数
のいずれの求め方も知っておく必要があります。
もし、1つでも知らないものがあれば、
必ずいますぐ確認してください。
問3(2)の平均値の求め方は大丈夫ですか?
これはできない人が必ずいると思います。
特に求め方を知っているのに、解き方がわからない的なことを
言っている人は要注意です。
小学生で平均の求め方は習いますが、
中学生でも、もう1つの平均の求め方を習います。
つまり、平均を求める方法は2種類あるということですね。
そうなの?なった受験生は、
上の解説をしっかり見といてください。
問4は連立方程式の文章問題ですね。
「少し文章が長い」と「割合が絡んでいる」
ことからできなかった人も多かったと思います。
特に割合でつまづいている場合、
小学生の内容でつまづいていることになるので
少し前に戻って勉強をしたほうがいいです。
遠回りをしているように感じるかもしれませんが、
絶対に近道なので、迷わずに前の勉強をしていってくださいね。
第三問
問1解説「規則性」☆☆

このような問題は、しっかり表を作って
状況を整理することが大事です。
そして、これができたら、
規則が何かないのかと探しましょう。
この規則に関して、
ある程度問題を解いていたら
どんな規則があるか経験でわかるようになってきます。
何でこの規則を見つけれるのかと思う人は、
1週間ほど、規則の問題を解きまくってみてください。
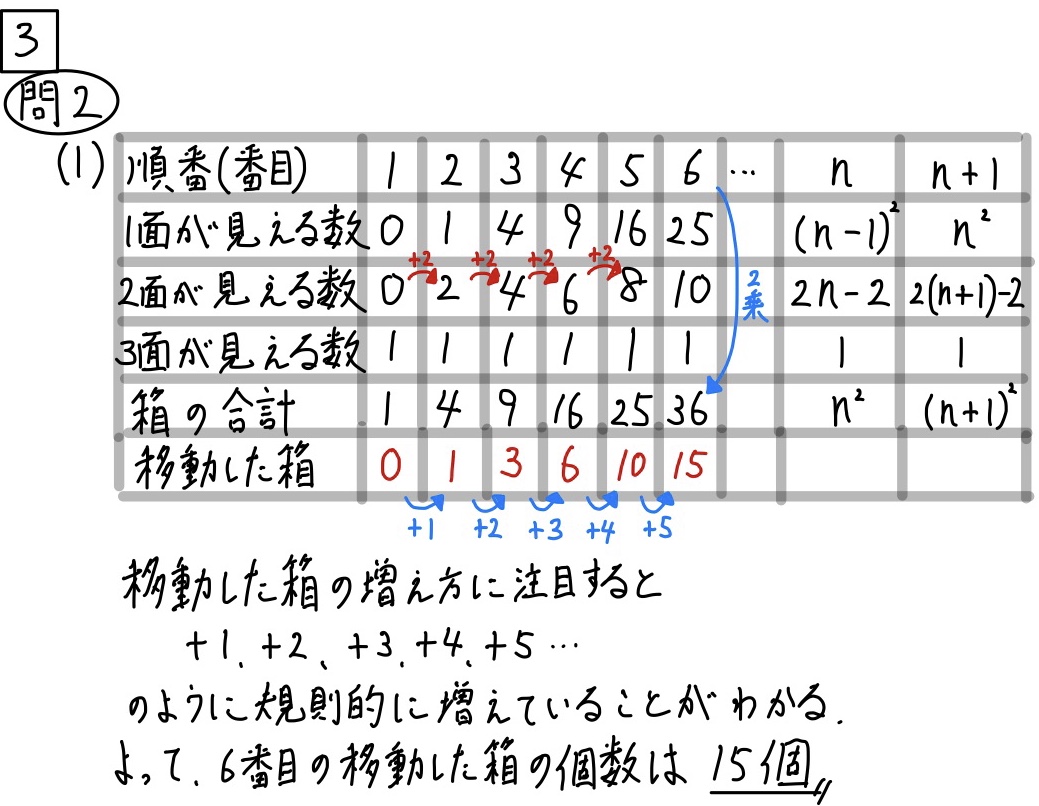
問2(1)解説「規則性」☆☆
この問題も移動した箱の数を
上の表のように書いてみると分かりやすいですね。
+1、+2、+3、+4、+5のように
増えていっていることが見て分かります。
よって、6番目に移動した箱の数は意外とすぐに見つけることができましたね。
問2(2)解説「規則性」☆☆☆

この問題も規則を見つけることが大事です。
規則を見つけることができれば、
x番目に関して
見えていない箱の個数は、xー1
箱の合計個数は、x^2
とすることができます。
ここができれば、解説のような方程式が立てれますね。
第四問
問1解説「二乗に比例する関数(変域)」☆☆

これは二乗に比例する関数のところで
最初に習う内容ですね。
グラフをイメージしながら解いていない人は、
ミスする人が多いです。
習いたての時は、必ずグラフを書いて解くことを
強くおすすめします。
問2解説「二乗に比例する関数(二等辺三角形)」☆☆

いろんな考え方あると思いますが、
僕はこんな風に考えて解きました。
鋭角や鈍角について考えながら解いている解説をみましたが、
そんなの考えながら解かないですね笑
でも、本当に勉強になりました。
これからしっかり取り入りきたいと思います。
問3解説「二乗に比例する関数(座標)」☆☆

こういう問題は、
解き方の流れをしっかり言えるように
なっておきましょう。
よく見る問題のはずなので、
必ずできるようになっといてくださいね。
解き方の流れを解説の通りです。
問4解説「二乗に比例する関数(比例定数)」☆☆☆

これは解き方を間違えちゃいました。
すみません笑
ただ、内容的には間違ってはいなくて、
もっと簡単に解けるやり方を見つけちゃいました笑
赤と緑の台形から赤の三角形を引けば
もっと簡単にできましたね。
何でこっちでやらなかったのか謎ですよね。
でも、解き方は1つしかないということを示せたので
これはこれでいいのかなと思います。
第五問
問1解説「合同(辺の長さ)」☆☆問2「おうぎ形の面積」☆☆

この2問は確実に正解したい問題ですね。
この問題に関しては、
問題を見たら解き方が思い浮かぶレベルまでに
なっておく必要があります。
これができるようになれば、
解くスピードが格段に上がっていきます。
じゃあ、何をやればいいのか。
問題をたくさん解くしかありません。
効率的に解けるようになるのは、
たくさん問題を解いて初めて身につくことです。
最初から効率的にしようなんて考えなくていいです。
まず、この問題から解き方が思い浮かぶようにしていきましょう!
問3(1)解説「相似の証明問題」☆☆

この問題は
円周角の定理
と
二等辺三角形
を利用して証明する問題です。
見た瞬間にこれは分かりません。
まず、考えることは
・どこの角が等しいのか
・どこの辺が等しいのか
です。
これを繰り返していくことで、
徐々に証明問題は解けるようになっていきます。
もちろん、合同条件や相似条件を
完璧に覚えていることは前提条件ですけどね。
問3(2)解説「平面図形の応用(辺の長さ)」☆☆☆

この問題は
相似を2回
三平方の定理を1回
を使って解く問題でした。
やはり、相似を2回使って解く問題になると
難しさが増してきますね。
上位校に合格するためには
ここが特に大事になってくるでしょう。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年和歌山県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。