
公開日2020/06/02
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題を見たい方は下のリンクからどうぞ。
さなる予備校のホームページ載っているので気になる方はこちらからどうぞ。
5年分くらいは解いておくべきなので、過去問を買うことをお勧めします。
第一問
(1)解説「計算問題」☆

今回の問題で特にいうことはないので、少し話をしたいと思います。
このあたりの問題を普通に正解するレベルに全員がなってほしい。
どんな学校を受験するにしても。
なぜなら中3の6月くらいまでに全て習う内容だから。
習ってから入試までに何ヶ月あるのだろうか。
それなのにできない状況であるのは、
勉強していない、もしくは、間違った勉強をしているに違いないです。
勉強していないのは当然できないけれど、問題なのは勉強しているのにできない生徒である。
特に決まりきったテキストがある塾に通っている場合は要注意です。
この場合、テキストの全内容をほとんど終わらせることに塾側が必死になっているはずです。
目的が
勉強して成績を上げたり、合格をすることだったりではなく、
テキストを終わらせることが目的になっているのです。
今回解説している問題すらできない場合、テキストを終わらせることを目的にしていたら時間の無駄でしかありません。
もしこのような状況になっていたら、塾側に入試問題の大問1、2のような問題をできるようにしてくださいと要望するといいですね。
もちろん、数学の話です。
理科や社会なら一問一答のページがあると思うので、そのページだけ何回も勉強すればいいです。
英語や国語は後回しでいいと思います。最悪、やらなくてもいいかも。
すぐに伸びる科目ではない上に、全部やろうとするとパンクしてしまうので。
もちろん、状況によって話は変わりますけどね。
第二問
(1)解説「コンパスを使った作図」☆☆

✖️印はコンパスの針を指す部分
この問題は2つ条件が与えられていて、それを読んでどんな線を引けばいいのか判断する必要があります。
それぞれ見ていきましょう。
①円の中心Oは、点Pを通り辺ACに垂直な直線上の点である。
→垂線を引く
②円Oは、2つの辺AB、ACの両方に接する
→角の二等分線を引く
こんな感じですね。
特に②が分からない人が毎年多いです。
なぜ分からない人が多いのか。
それは、角の二等分線を単に
『角度を半分にする線』
だと思っているから。
分からない人は、教科書などで調べましょう。
それでも分からなければググりましょう。
それでも分からなければ、先生に聞きに行ってください。
自分で動いて理解しないと覚えられません。
頑張ってくださいね。
(1)解説「コンパスを使った作図」アニメーション
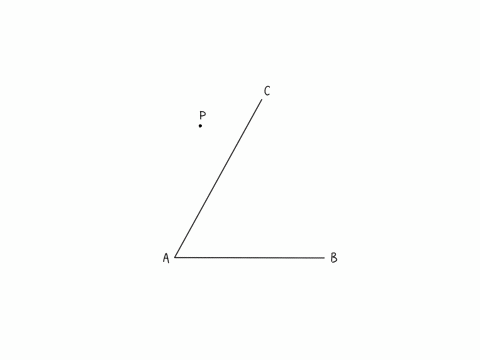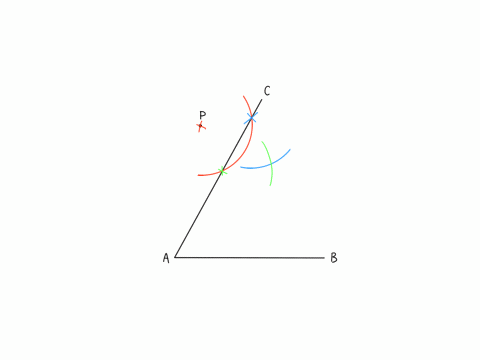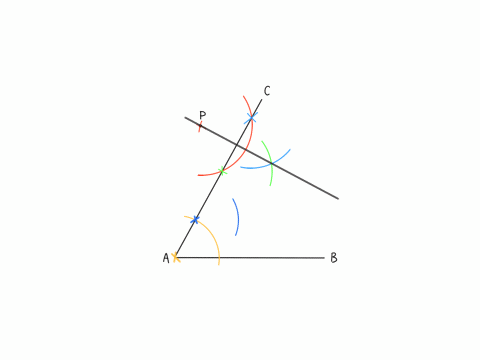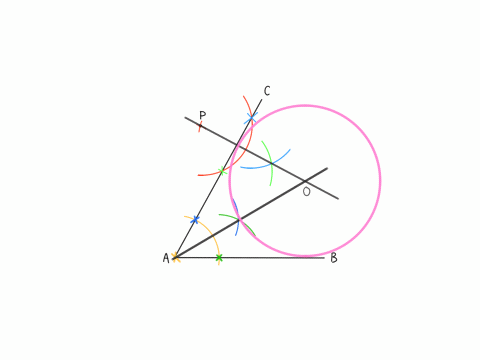
✖️印はコンパスの針を刺す部分
最後の円は描く必要はありません。
直線と円が接することを示しただけです。
(2)解説「おうぎ形の角度」☆☆

この問題は苦戦する人が多いですね。
しかし、解答にたどり着くまでの手順は多くないです。
上のポイントみたいに、まず、比の解き方を覚えてしまいましょう。
数学が苦手なら理解なんて後回しでいいです。
覚えましょう。
少しずつ解ける問題が増えていきます。
そしたら、いつの間にか理解していますよ。
数学なんてそんなもんです。
もちろん、レベルが上がれば大変ですけどね笑
(3)解説「確率」☆
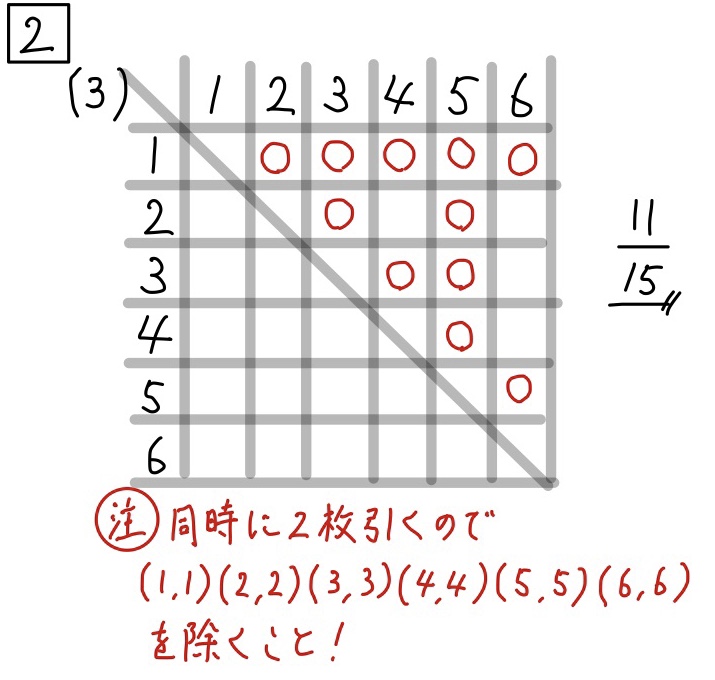
この問題では表の使い方に注意しましょう。
引いた数字が、〔1、2〕〔2、1〕のどちらの順番でも意味は変わりませんよね。
こういうときは、上半分だけ使いましょう。
(下半分でも構いません。)
では、どういう時に全体を使うのか。
それは、
〔十の位、一の位〕=〔2、1〕、〔1、2〕
〔大きいサイコロ、小さい頃〕=〔2、1〕、〔1、2〕
のような時です。
これだと、意味が完全に変わってきますよね。
こういうところまで意識して解くようにしましょう。
第三問
(1)解説「資料の整理(最頻値)」☆(2)「資料の整理(範囲)」☆☆☆

(1)は日数の最頻値を求めるので、答えの単位は『日』です。
これが分かっていたら、間違いはかなり減ると思います。
答えとしては、16日か7日のどちらかに絞られますね。
ただ、最頻値という言葉の意味が分かっていれば、間違わないはずです。
最頻値は、最も頻繁に起こる値ってことです。
つまり、7日が4回もあった訳なので答えは7日に決まりですね。
(2)は難しいです。
しっかり状況を理解できないと解くことはできないと思います。
範囲が12なので、現状の数字より小さかったり、大きかったりすることはないです。
だから、aは4以上16未満ってことになります。
また、中央値は8.5です。
つまり、7と10の間に中央値がこなければなりません。
そして、中央値は真ん中なので6.5番目にあるのですが、aの値を決まる前に現時点で7と10の間に中央値が来ていることになります。
だから、aが10以上じゃないと中央値は8.5にならないのです。
このことから、答えは10以上16未満となりましたね。
うーん、難しいです。
上位校を目指す人はできるようになってほしい内容です。
第四問
解説「連立方程式の文章題(割合)」☆☆

割合の内容になると拒否反応を示す人が多くなりますね。
まあ、難しいのは分かります。
しかし、ここが苦手な場合、中学生内容が分からないというより小学生の内容でつまづいているのです。
おそらくというか、確実に小学生の割合の問題が解けないと思います。
中学生の人で割合が苦手な人は、小学校の教科書を引っ張り出してきて割合の問題を解いてみてください
きっと解けない問題が出てきます。
その出来なかった問題をできるようにしてから、この問題に戻ってきてください。
そしたら、いきなり解くことは出来ないかもしれないですが、わかるようになっているはずです。
分かるようになったら、解き方を丸暗記しちゃいましょう。
そしたら、ある程度の問題は解けるようになっちゃいます。
頑張ってくださいね。
第五問
(1)解説「ねじれの位置」☆(2)「空間図形(辺の長さ)」☆☆

(1)は平行、かつ、ねじれの位置を求める問題ですね。
あんまり見たことないかもしれませんが、解き方は何も変わりません。
しっかり正解したいところですね。
(2)は三平方の定理を使うだけの問題です。
平面図形の問題が苦手な人は、こういう問題をまずしっかり解けるようにしましょう。
こういう問題が解けないことには、数学の点数は上がってきません。
もちろん、これが出来たからといってすぐに点数は上がりません。
しかし、あくまで平面図形ができるようになる入り口と思ってくれたらいいですね。
頑張って点数をあげれるようにしていきましょう。
(3)解説「空間図形(体積)」☆☆☆

この問題はかなり難しかったですね。
この問題は、上の解説のように
四角形MIJNを考える
ことがポイントでした。
ここが出来なければ、出来なかったですね。
そして、ここができた後に平行線と比をを使って、
ML:LKの比
を求めるのも難しかったかもしれませんね。
この2点を乗り越えることができれば、解答にたどり着いたことでしょう。
この問題は、難しいと思いますが、
上位校を目指す人はしっかりできるようになってほしいです。
この辺りができないと、合格は難しいと思ってもらっても構わないですね。
第六問
(1)解説「反比例」☆(2)「変化の割合」☆☆

この問題は、見た目が難しそうですよね笑
でも、ひるまないでくださいね笑
(1)(2)は難しくありません。
どっちかというと、基本的な問題ですね。
反比例の式と変化の割合を求めるだけなので。
どんな問題でも、まず考えてみましょう。
最初の問題は簡単なことが多いです。
どんなに数学が苦手であっても、(1)は必ず正解するんだ!という気持ちを持ち続けてくださいね。
(3)解説「関数と図形」☆☆☆

この問題も難しいかと言えば、正直そこまでじゃないです。
(1)(2)よりは難しいですけど。
ただ、やることは四角形BFAEや三角形ADFの各頂点の座標は求めるだけです。
ここを乗り越えたら、もう解けたようなもんです。
あと、座標を求めずに、分かりませんとかあり得ませんからね。
こんな状態で質問きたら、少し叱って突き返します笑
こんな状態で考えているはずがないのでね笑
このレベルはしっかりできてほしいので頑張ってくださいね!
第七問
(1)解説「相似の証明」☆☆☆

この証明は、難しいです。
見てもらったらわかると思いますが、長いですよね笑
この問題は、最後までの道筋がしっかり見えてなければ飛ばしてもいいかもしれません。
ただ、途中まで書いて部分点狙いに切り替えるのもありかもしれませんね。
この問題に時間を使って、時間が足りなくなったということは絶対に避けましょう。
だから、難しいと判断すれば飛ばす判断はありです。
逃げているのではなく、勇気ある判断なんですから。
(2)解説「平面図形の応用(相似)」☆☆

1つ覚えておいてほしいことがあります。
最初に証明問題があれば、その証明を使って次の問題を解くことが非常に多いです。
もちろん、絶対ではありません。
今回の問題は、さっき証明したことを使っています。
仮に証明が分からなかったとしても、この問題で当然使っていいですからね笑
どんどん使いましょう。
そして、この問題が難しいのは、新たな相似を使って解かなければならないこと。
大阪の入試問題にもこのタイプはよく出ていますね!
このレベルができるようになれば上位校に確実に合格できるでしょう。
一歩ずつ頑張っていきましょうね!
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年静岡県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。