
公開日2020/05/21
どうも、塾講師のこうです。
解説画像だけでなく、
解き方の流れ、考え方、覚えるべきポイント
もお伝えしていきます。
↑↑↑↑↑↑↑↑↑↑
全国の入試問題を少しずつ解説しています。
また、大阪の公立高校入試倍率、大学合格実績、部活動について書いています。
気になる方はクリックしてみてください。
僕は勉強が苦手で、努力で乗り切ってきたタイプです。
そんな僕だからこそ、勉強が苦手な人にとって分かりやすい内容になっているのではないかと思います。
※できる人にとったらまわりくどく感じるかもしれません。そんな人はそっとこのページを閉じてくださいね笑
また、問題集の解説がどうしても分かりにくいなーって思った経験ありませんか?
僕はあります。
この経験があって、ブログにもっと分かりやすい解説を載せようと思いました。
ぜひ少しでも多くの方の参考になればなと思います。
解説している問題を見たい方は下のリンクからどうぞ。
東京新聞:2020年首都圏公立高校入試(TOKYO Web)
※一定期間が過ぎるとリンクが切れている可能性があります。
第一問
(1)〜(6)解説「計算問題」☆

ここは基本的な問題ばかりです。
符号ミス、計算間違い、見間違いをしないように常に気をつけましょう。
そして、常にミスはするものだという意識は持っておきましょう。
(7)解説「連立方程式」☆(8)「解の公式」☆

(7)(8)ともに基本的な問題です。
しかし、どちらもミスが比較的起こりやすい問題です。
特に『解の公式』は計算ミスが多いです。
具体的には、『解の公式』中のbの部分がマイナスの時にミスが起きやすいです。
だから、bがマイナスだと分かれば気を引き締めて問題に取り組んでほしいですね。
(9)解説「角度」☆(10)「変化の割合」☆

(9)は超定番問題です。
問題のような形をみたら、一本補助線を引きたくてたまらないようになってほしいですね笑
そして、これさえできれば、錯角を使うだけです。
(10)も定番問題ですね。
しかし、間違う人も少しいます。
特に答えを『2』とした人は要注意です。
一次関数と二乗に比例する関数の違いがわかっていないはずです
これに関して、自分で違いに気付くのは難しいと思うので、先生に
「一次関数と二乗に比例する関数の傾きの違いを教えてください」
と聞いてみてください。
(11)解説「ねじれの位置」☆(12)「反比例・点対称・変化の割合」☆☆
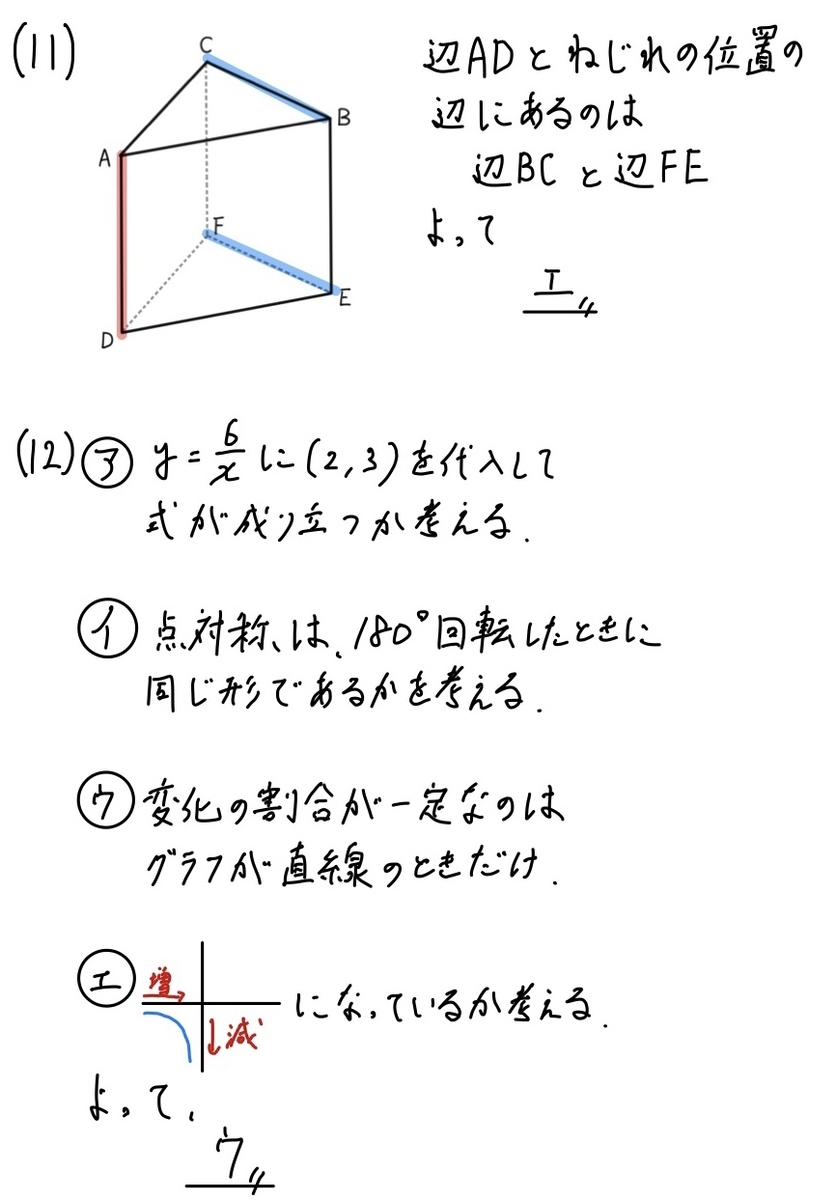
(11)のねじれの問題は入試でよく見かけます。
理解していれば難しくないので、全員ができないといけません。
(12)は問題文をしっかり読んでくださいね。
間違っているものを選ばなくてはいけません。
答えを選ぶのは比較的難しくないと思います。
ただ、間違っている理由をしっかり答えられる人は多くないと思います。
正解はウです。
理由は、変化の割合は一定ではないから。
変化の割合が一定になるのは、直線の場合のみです。
つまり、反比例で変化の割合が一定になることはありえません。
(13)解説「円錐の高さと体積」☆☆

これは確実に正解したい問題ですね。
三平方の定理、円錐の体積の求め方は必ず即答できるようにしておきましょう。
特に、体積の1/3を掛け忘れないように注意してください!
また、今回問題にはなっていませんが、円錐の側面積を求めるのを苦手にしている人が多いです。
だから、側面積もしっかり求めることができるようになっておきましょう。
(14)解説「確率」☆☆(15)「平均値・中央値」☆(16)「全数調査」☆

(14)のような確率の問題は表を書いて解くようにしましょう。
もちろん、樹形図で解くべき時も多々あります。
しかし、経験上、表で解いた方がミスなく早くできます。
(15)平均値の求め方は特に問題ないと思います。
ただ、平均値の求め方は2種類あります。
問題によって、使い分ける必要があるので
「???」ってなっている人は必ず確認しておきましょう。
そして、中央値の求め方を分かっていない人は結構多いです。
中央値を求めるためには、小さい順、もしくは、大きい順に並び替える必要があります。
この作業をした時の真ん中の数値が中央値です。
覚えておいてくださいね。
(16)は正解率が意外と低そうな問題ですね。
選択肢は選べると思いますが、その理由を答えるのは少し難しいです。
標本調査と全数調査の仕方は教科書を見て答えられるようにしましょう。
そして、標本調査と全数調査は次のように使い分けます。
標本調査は、全体の数が多すぎるとき
全数調査は、全体の数がそこまで多くないとき(例えば、学校のような集団)
大まかな説明ですが、これくらいの考えで十分です。
覚えておいてくださいね。
第二問
(1)解説「コンパスを使った作図」☆

✖️印はコンパスの針を指す部分
これは最初に習う垂線の引き方そのものです。
知っているかどうかの問題で、必ず正解しなくてはいけません。
(1)解説「コンパスを使った作図」アニメーション

✖️印はコンパスの針を指す部分
(2)解説「合同の証明問題」

東京新聞さんに載っている解説と変えてみました。
かなりまわりくどいやり方になりましたが、あー、こういう証明をしないとダメな時もあるなって思ってくれたら嬉しいです。
ただ、この問題では直角三角形で証明する方が断然楽です笑
直角三角形の証明を見たい方はこちらをどうぞ。
第三問
(1)解説「相似比」☆(2)「三平方の定理」☆☆

この問題は中学受験の問題にそのまま出てきそうですね笑
小学生でこういう問題を解けるようになっているのはやっぱりすごいですよね。
でも、中学受験の勉強をしていたらみんなできるようになるのかと言えば、それは違います。
子どもによって、伸びる時期というものがありますしね。
あと、やってもできないという子どもが一定数いることを心のどこかに置いておきたい。
もちろんそんな状況でも何もやらせないわけじゃない。
根気強く接することが本当に大事。
そしたら、ほんの少しずつだけど、必ず成果は目に見えてくる。
もしかしたら、ある人にとって、その成果は意味があるように見えないかもしれない。
でも、その子にとったら大きな一歩であることに変わりはない。
僕はその子にとっての大きな一歩に関わり続けたいと思う。
今回の問題は特にいうことはなかったので、僕の考えを少し書いてみました。
第四問
(1)解説「直線の式」☆☆

関数のグラフ問題では1問目に直線の式が問われることが非常に多いです。
ただ、問題になってなくても求める必要がある場合も多々あります。
必ずできるようにならなければなりません。
この問題ができてなければ、B問題採用校に合格することは無理だと思って構いません。
(2)①解説「関数の応用(座標)」☆☆

問題集によく載っているような定番問題です。
でも、解き方はなんとなく分かっているけどできない人が多い問題でもあります。
関数で正方形の問題は、
縦と横の辺を文字で表して、それを=(イコール)で結べばいい
ことを頭の中に入れておいてほしいですね。
これは決まりきった問題の解き方です。
つまり、今までやってきた問題をしっかりできるようにしてきたかが問われているわけです。
問題はたくさん解く必要はあります。
しかし、解くだけでできるようにしていなければ意味がありません。
分かれない問題を確実にできるようにしていきましょう。
ここで注意してほしいのが、明らかに難しすぎる問題はする必要はありません。
真面目な子ほど陥りやすいですが、ここで時間がかかって挫折してしまいます。
ある程度できたらいいという意識は持つ必要がありますね。
(2)②解説「関数の応用(座標)」☆☆☆

この問題は難しいですね。
ただ、難易度☆☆☆☆まではいかないかなって感じです。
まず、難しいいのは載っている図だけでは解けないというところですね。
自分で図を描いて考える必要があります。
その図は解説の右側ですね。
点Qの場所は決まっていないないので動くのです。
このタイプの問題を解く機会はかなり少ないので、ここまで仕上げるのは難しいです。
数学が少し得意くらいじゃ無理でしょう。
でも、上位校を合格していく人には、ぜひとも解けるようになってほしい問題です。
なぜなら高校では、このような問題は普通に出てくるからです。
先を見据えた勉強をするといいですね。
でも、中学生が先の勉強なんて知っているはずありません。
こういうところで塾の先生に一言二言アドバイスをもらえると本当はいいんですけどね。
難易度☆マークの説明
難易度の説明
☆:全員解けなければならない問題
☆☆:標準問題(B問題採用校受験の人は解けるようにすべき問題)
☆☆☆:応用問題(C問題採用校受験の人は解けるようにすべき問題)
☆☆☆☆:チャレンジ問題(解けなくても合格できるであろう問題)
大阪の受験生向け
A問題採用校受験の人は、☆の問題のみ解いていきましょう。
B問題採用校受験の人は、☆と☆☆の問題をまず解けるようにして、余裕があれば☆☆☆まで解けるようにすると最高です。
C問題採用受験の人は、☆~☆☆☆を全部解けるようにしましょう。そして、できなくてもいいので☆☆☆☆は必ずチャレンジしてください。
日本全国の高校入試数学の解説を見たい方
上位校は目指す人は必ず日本全国の入試問題にチャレンジするべきです!
今回は2020年埼玉県公立高校入試数学をお伝えしました。
これから少しずつ公開していきますので、参考になる方が1人でもいれば嬉しいです。
数ある中の1つの意見として読んでいただければと思います。
最後まで読んでいただきありがとうございました。